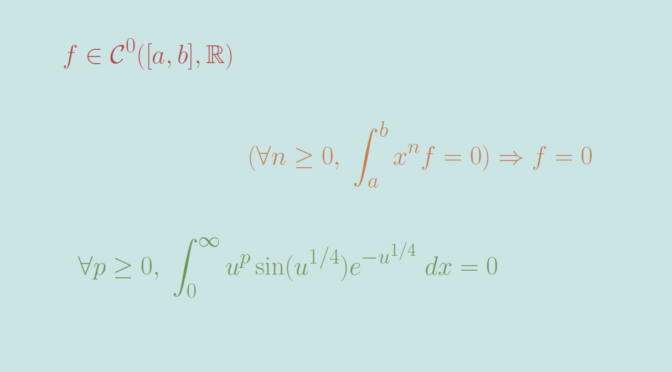Tag Archives: real-analysis

Analysis

A semi-continuous function with a dense set of points of discontinuity

Leave a comment

Let’s come back to Thomae’s function which is defined as:
\[f:
\left|\begin{array}{lrl}
\mathbb{R} & \longrightarrow & \mathbb{R} \\
x & \longmapsto & 0 \text{ if } x \in \mathbb{R} \setminus \mathbb{Q} \\
\frac{p}{q} & \longmapsto & \frac{1}{q} \text{ if } \frac{p}{q} \text{ in lowest terms and } q > 0
\end{array}\right.\]

We proved here that \(f\) right-sided and left-sided limits vanish at all points. Therefore \(\limsup\limits_{x \to a} f(x) \le f(a)\) at every point \(a\) which proves that \(f\) is upper semi-continuous on \(\mathbb R\). However \(f\) is continuous at all \(a \in \mathbb R \setminus \mathbb Q\) and discontinuous at all \(a \in \mathbb Q\).

Analysis

Converse of fundamental theorem of calculus

Leave a comment

The fundamental theorem of calculus asserts that for a continuous real-valued function \(f\) defined on a closed interval \([a,b]\), the function \(F\) defined for all \(x \in [a,b]\) by
\[F(x)=\int _{a}^{x}\!f(t)\,dt\] is uniformly continuous on \([a,b]\), differentiable on the open interval \((a,b)\) and \[
F^\prime(x) = f(x)\]
for all \(x \in (a,b)\).

The converse of fundamental theorem of calculus is not true as we see below.

Consider the function defined on the interval \([0,1]\) by \[
f(x)= \begin{cases}
2x\sin(1/x) – \cos(1/x) & \text{ for } x \neq 0 \\
0 & \text{ for } x = 0 \end{cases}\] \(f\) is integrable as it is continuous on \((0,1]\) and bounded on \([0,1]\). Then \[
F(x)= \begin{cases}
x^2 \sin \left( 1/x \right) & \text{ for } x \neq 0 \\
0 & \text{ for } x = 0 \end{cases}\] \(F\) is differentiable on \([0,1]\). It is clear for \(x \in (0,1]\). \(F\) is also differentiable at \(0\) as for \(x \neq 0\) we have \[
\left\vert \frac{F(x) – F(0)}{x-0} \right\vert = \left\vert \frac{F(x)}{x} \right\vert \le \left\vert x \right\vert.\] Consequently \(F^\prime(0) = 0\).

However \(f\) is not continuous at \(0\) as it does not have a right limit at \(0\).

Analysis

Counterexamples around series (part 2)

Leave a comment

We follow the article counterexamples around series (part 1) providing additional funny series examples.

If \(\sum u_n\) converges and \((u_n)\) is non-increasing then \(u_n = o(1/n)\)?

This is true. Let’s prove it.
The hypotheses imply that \((u_n)\) converges to zero. Therefore \(u_n \ge 0\) for all \(n \in \mathbb N\). As \(\sum u_n\) converges we have \[
\displaystyle \lim\limits_{n \to \infty} \sum_{k=n/2}^{n} u_k = 0.\] Hence for \(\epsilon \gt 0\), one can find \(N \in \mathbb N\) such that \[
\epsilon \ge \sum_{k=n/2}^{n} u_k \ge \frac{1}{2} (n u_n) \ge 0\] for all \(n \ge N\). Which concludes the proof.

\(\sum u_n\) convergent is equivalent to \(\sum u_{2n}\) and \(\sum u_{2n+1}\) convergent?

Is not true as we can see taking \(u_n = \frac{(-1)^n}{n}\). \(\sum u_n\) converges according to the alternating series test. However for \(n \in \mathbb N\) \[
\sum_{k=1}^n u_{2k} = \sum_{k=1}^n \frac{1}{2k} = 1/2 \sum_{k=1}^n \frac{1}{k}.\] Hence \(\sum u_{2n}\) diverges as the harmonic series diverges.

\(\sum u_n\) absolutely convergent is equivalent to \(\sum u_{2n}\) and \(\sum u_{2n+1}\) absolutely convergent?

This is true and the proof is left to the reader.

\(\sum u_n\) is a positive convergent series then \((\sqrt[n]{u_n})\) is bounded?

Is true. If not, there would be a subsequence \((u_{\phi(n)})\) such that \(\sqrt[\phi(n)]{u_{\phi(n)}} \ge 2\). Which means \(u_{\phi(n)} \ge 2^{\phi(n)}\) for all \(n \in \mathbb N\) and implies that the sequence \((u_n)\) is unbounded. In contradiction with the convergence of the series \(\sum u_n\).

If \((u_n)\) is strictly positive with \(u_n = o(1/n)\) then \(\sum (-1)^n u_n\) converges?

It does not hold as we can see with \[
u_n=\begin{cases} \frac{1}{n \ln n} & n \equiv 0 [2] \\
\frac{1}{2^n} & n \equiv 1 [2] \end{cases}\] Then for \(n \in \mathbb N\) \[
\sum_{k=1}^{2n} (-1)^k u_k \ge \sum_{k=1}^n \frac{1}{2k \ln 2k} – \sum_{k=1}^{2n} \frac{1}{2^k} \ge \sum_{k=1}^n \frac{1}{2k \ln 2k} – 1.\] As \(\sum \frac{1}{2k \ln 2k}\) diverges as can be proven using the integral test with the function \(x \mapsto \frac{1}{2x \ln 2x}\), \(\sum (-1)^n u_n\) also diverges.

Analysis

A nonzero continuous map orthogonal to all polynomials

1 Comment

Let’s consider the vector space \(\mathcal{C}^0([a,b],\mathbb R)\) of continuous real functions defined on a compact interval \([a,b]\). We can define an inner product on pairs of elements \(f,g\) of \(\mathcal{C}^0([a,b],\mathbb R)\) by \[
\langle f,g \rangle = \int_a^b f(x) g(x) \ dx.\]

It is known that \(f \in \mathcal{C}^0([a,b],\mathbb R)\) is the always vanishing function if we have \(\langle x^n,f \rangle = \int_a^b x^n f(x) \ dx = 0\) for all integers \(n \ge 0\). Let’s recall the proof. According to Stone-Weierstrass theorem, for all \(\epsilon >0\) it exists a polynomial \(P\) such that \(\Vert f – P \Vert_\infty \le \epsilon\). Then \[
\begin{aligned}
0 &\le \int_a^b f^2 = \int_a^b f(f-P) + \int_a^b fP\\
&= \int_a^b f(f-P) \le \Vert f \Vert_\infty \epsilon(b-a)
\end{aligned}\] As this is true for all \(\epsilon > 0\), we get \(\int_a^b f^2 = 0\) and \(f = 0\).

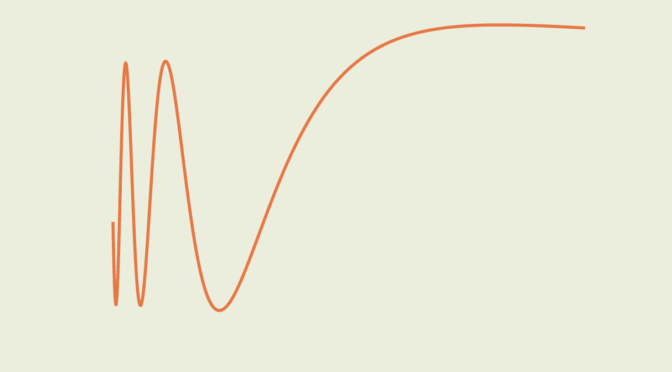
We now prove that the result becomes false if we change the interval \([a,b]\) into \([0, \infty)\), i.e. that one can find a continuous function \(f \in \mathcal{C}^0([0,\infty),\mathbb R)\) such that \(\int_0^\infty x^n f(x) \ dx\) for all integers \(n \ge 0\). In that direction, let’s consider the complex integral \[
I_n = \int_0^\infty x^n e^{-(1-i)x} \ dx.\] \(I_n\) is well defined as for \(x \in [0,\infty)\) we have \(\vert x^n e^{-(1-i)x} \vert = x^n e^{-x}\) and \(\int_0^\infty x^n e^{-x} \ dx\) converges. By integration by parts, one can prove that \[
I_n = \frac{n!}{(1-i)^{n+1}} = \frac{(1+i)^{n+1}}{2^{n+1}} n! = \frac{e^{i \frac{\pi}{4}(n+1)}}{2^{\frac{n+1}{2}}}n!.\] Consequently, \(I_{4p+3} \in \mathbb R\) for all \(p \ge 0\) which means \[
\int_0^\infty x^{4p+3} \sin(x) e^{-x} \ dx =0\] and finally \[
\int_0^\infty u^p \sin(u^{1/4}) e^{-u^{1/4}} \ dx =0\] for all integers \(p \ge 0\) using integration by substitution with \(x = u^{1/4}\). The function \(u \mapsto \sin(u^{1/4}) e^{-u^{1/4}}\) is one we were looking for.

Analysis

Counterexamples on real sequences (part 3)

Leave a comment

This article is a follow-up of Counterexamples on real sequences (part 2).

Let \((u_n)\) be a sequence of real numbers.

If \(u_{2n}-u_n \le \frac{1}{n}\) then \((u_n)\) converges?

This is wrong. The sequence
\[u_n=\begin{cases} 0 & \text{for } n \notin \{2^k \ ; \ k \in \mathbb N\}\\
1- 2^{-k} & \text{for } n= 2^k\end{cases}\]
is a counterexample. For \(n \gt 2\) and \(n \notin \{2^k \ ; \ k \in \mathbb N\}\) we also have \(2n \notin \{2^k \ ; \ k \in \mathbb N\}\), hence \(u_{2n}-u_n=0\). For \(n = 2^k\) \[
0 \le u_{2^{k+1}}-u_{2^k}=2^{-k}-2^{-k-1} \le 2^{-k} = \frac{1}{n}\] and \(\lim\limits_{k \to \infty} u_{2^k} = 1\). \((u_n)\) does not converge as \(0\) and \(1\) are limit points.

If \(\lim\limits_{n} \frac{u_{n+1}}{u_n} =1\) then \((u_n)\) has a finite or infinite limit?

This is not true. Let’s consider the sequence
\[u_n=2+\sin(\ln n)\] Using the inequality \(
\vert \sin p – \sin q \vert \le \vert p – q \vert\)
which is a consequence of the mean value theorem, we get \[
\vert u_{n+1} – u_n \vert = \vert \sin(\ln (n+1)) – \sin(\ln n) \vert \le \vert \ln(n+1) – \ln(n) \vert\] Therefore \(\lim\limits_n \left(u_{n+1}-u_n \right) =0\) as \(\lim\limits_n \left(\ln(n+1) – \ln(n)\right) = 0\). And \(\lim\limits_{n} \frac{u_{n+1}}{u_n} =1\) because \(u_n \ge 1\) for all \(n \in \mathbb N\).

I now assert that the interval \([1,3]\) is the set of limit points of \((u_n)\). For the proof, it is sufficient to prove that \([-1,1]\) is the set of limit points of the sequence \(v_n=\sin(\ln n)\). For \(y \in [-1,1]\), we can pickup \(x \in \mathbb R\) such that \(\sin x =y\). Let \(\epsilon > 0\) and \(M \in \mathbb N\) , we can find an integer \(N \ge M\) such that \(0 < \ln(n+1) - \ln(n) \lt \epsilon\) for \(n \ge N\). Select \(k \in \mathbb N\) with \(x +2k\pi \gt \ln N\) and \(N_\epsilon\) with \(\ln N_\epsilon \in (x +2k\pi, x +2k\pi + \epsilon)\). This is possible as \((\ln n)_{n \in \mathbb N}\) is an increasing sequence and the length of the interval \((x +2k\pi, x +2k\pi + \epsilon)\) is equal to \(\epsilon\). We finally get \[ \vert u_{N_\epsilon} - y \vert = \vert \sin \left(\ln N_\epsilon \right) - \sin \left(x + 2k \pi \right) \vert \le \left(\ln N_\epsilon - (x +2k\pi)\right) \le \epsilon\] proving that \(y\) is a limit point of \((u_n)\).

Analysis

A strictly increasing continuous function that is differentiable at no point of a null set

Leave a comment

We build in this article a strictly increasing continuous function \(f\) that is differentiable at no point of a null set \(E\). The null set \(E\) can be chosen arbitrarily. In particular it can have the cardinality of the continuum like the Cantor null set.

A set of strictly increasing continuous functions

For \(p \lt q\) two real numbers, consider the function \[
f_{p,q}(x)=(q-p) \left[\frac{\pi}{2} + \arctan{\left(\frac{2x-p-q}{q-p}\right)}\right]\] \(f_{p,q}\) is positive and its derivative is \[
f_{p,q}^\prime(x) = \frac{2}{1+\left(\frac{2x-p-q}{q-p}\right)^2}\] which is always strictly positive. Hence \(f_{p,q}\) is strictly increasing. We also have \[
\lim\limits_{x \to -\infty} f_{p,q}(x) = 0 \text{ and } \lim\limits_{x \to \infty} f_{p,q}(x) = \pi(q-p).\] One can notice that for \(x \in (p,q)\), \(f_{p,q}^\prime(x) \gt 1\). Therefore for \(x, y \in (p,q)\) distinct we have according to the mean value theorem \(\frac{f_{p,q}(y)-f_{p,q}(x)}{y-x} \ge 1\).

Covering \(E\) with an appropriate set of open intervals

As \(E\) is a null set, for each \(n \in \mathbb N\) one can find an open set \(O_n\) containing \(E\) and measuring less than \(2^{-n}\). \(O_n\) can be written as a countable union of disjoint open intervals as any open subset of the reals. Then \(I=\bigcup_{m \in \mathbb N} O_m\) is also a countable union of open intervals \(I_n\) with \(n \in \mathbb N\). The sum of the lengths of the \(I_n\) is less than \(1\). Continue reading A strictly increasing continuous function that is differentiable at no point of a null set →

Analysis

A function whose Maclaurin series converges only at zero

Leave a comment

Let’s describe a real function \(f\) whose Maclaurin series converges only at zero. For \(n \ge 0\) we denote \(f_n(x)= e^{-n} \cos n^2x\) and \[
f(x) = \sum_{n=0}^\infty f_n(x)=\sum_{n=0}^\infty e^{-n} \cos n^2 x.\] For \(k \ge 0\), the \(k\)th-derivative of \(f_n\) is \[
f_n^{(k)}(x) = e^{-n} n^{2k} \cos \left(n^2 x + \frac{k \pi}{2}\right)\] and \[
\left\vert f_n^{(k)}(x) \right\vert \le e^{-n} n^{2k}\] for all \(x \in \mathbb R\). Therefore \(\displaystyle \sum_{n=0}^\infty f_n^{(k)}(x)\) is normally convergent and \(f\) is an indefinitely differentiable function with \[
f^{(k)}(x) = \sum_{n=0}^\infty e^{-n} n^{2k} \cos \left(n^2 x + \frac{k \pi}{2}\right).\] Its Maclaurin series has only terms of even degree and the absolute value of the term of degree \(2k\) is \[
\left(\sum_{n=0}^\infty e^{-n} n^{4k}\right)\frac{x^{2k}}{(2k)!} > e^{-2k} (2k)^{4k}\frac{x^{2k}}{(2k)!} > \left(\frac{2kx}{e}\right)^{2k}.\] The right hand side of this inequality is greater than \(1\) for \(k \ge \frac{e}{2x}\). This means that for any nonzero \(x\) the Maclaurin series for \(f\) diverges.

Analysis

Uniform continuous function but not Lipschitz continuous

Leave a comment

Consider the function \[
\begin{array}{l|rcl}
f : & [0,1] & \longrightarrow & [0,1] \\
& x & \longmapsto & \sqrt{x} \end{array}\]

\(f\) is continuous on the compact interval \([0,1]\). Hence \(f\) is uniform continuous on that interval according to Heine-Cantor theorem. For a direct proof, one can verify that for \(\epsilon > 0\), one have \(\vert \sqrt{x} – \sqrt{y} \vert \le \epsilon\) for \(\vert x – y \vert \le \epsilon^2\).

However \(f\) is not Lipschitz continuous. If \(f\) was Lipschitz continuous for a Lipschitz constant \(K > 0\), we would have \(\vert \sqrt{x} – \sqrt{y} \vert \le K \vert x – y \vert\) for all \(x,y \in [0,1]\). But we get a contradiction taking \(x=0\) and \(y=\frac{1}{4 K^2}\) as \[
\vert \sqrt{x} – \sqrt{y} \vert = \frac{1}{2 K} > \frac{1}{4 K} = K \vert x – y \vert\]

Analysis

Counterexamples around Cauchy condensation test

1 Comment

According to Cauchy condensation test: for a non-negative, non-increasing sequence \((u_n)_{n \in \mathbb N}\) of real numbers, the series \(\sum_{n \in \mathbb N} u_n\) converges if and only if the condensed series \(\sum_{n \in \mathbb N} 2^n u_{2^n}\) converges.

The test doesn’t hold for any non-negative sequence. Let’s have a look at counterexamples.

A sequence such that \(\sum_{n \in \mathbb N} u_n\) converges and \(\sum_{n \in \mathbb N} 2^n u_{2^n}\) diverges

Consider the sequence \[
u_n=\begin{cases}
\frac{1}{n} & \text{ for } n \in \{2^k \ ; \ k \in \mathbb N\}\\
0 & \text{ else} \end{cases}\] For \(n \in \mathbb N\) we have \[
0 \le \sum_{k = 1}^n u_k \le \sum_{k = 1}^{2^n} u_k = \sum_{k = 1}^{n} \frac{1}{2^k} < 1,\] therefore \(\sum_{n \in \mathbb N} u_n\) converges as its partial sums are positive and bounded above. However \[\sum_{k=1}^n 2^k u_{2^k} = \sum_{k=1}^n 1 = n,\] so \(\sum_{n \in \mathbb N} 2^n u_{2^n}\) diverges.

A sequence such that \(\sum_{n \in \mathbb N} v_n\) diverges and \(\sum_{n \in \mathbb N} 2^n v_{2^n}\) converges

Consider the sequence \[
v_n=\begin{cases}
0 & \text{ for } n \in \{2^k \ ; \ k \in \mathbb N\}\\
\frac{1}{n} & \text{ else} \end{cases}\] We have \[
\sum_{k = 1}^{2^n} v_k = \sum_{k = 1}^{2^n} \frac{1}{k} – \sum_{k = 1}^{n} \frac{1}{2^k} > \sum_{k = 1}^{2^n} \frac{1}{k} -1\] which proves that the series \(\sum_{n \in \mathbb N} v_n\) diverges as the harmonic series is divergent. However for \(n \in \mathbb N\), \(2^n v_{2^n} = 0 \) and \(\sum_{n \in \mathbb N} 2^n v_{2^n}\) converges.

Analysis

Pointwise convergence not uniform on any interval

Leave a comment

We provide in this article an example of a pointwise convergent sequence of real functions that doesn’t converge uniformly on any interval.

Let’s consider a sequence \((a_p)_{p \in \mathbb N}\) enumerating the set \(\mathbb Q\) of rational numbers. Such a sequence exists as \(\mathbb Q\) is countable.

Now let \((g_n)_{n \in \mathbb N}\) be the sequence of real functions defined on \(\mathbb R\) by \[
g_n(x) = \sum_{p=1}^{\infty} \frac{1}{2^p} f_n(x-a_p)\] where \(f_n : x \mapsto \frac{n^2 x^2}{1+n^4 x^4}\) for \(n \in \mathbb N\).

\(f_n\) main properties

\(f_n\) is a rational function whose denominator doesn’t vanish. Hence \(f_n\) is indefinitely differentiable. As \(f_n\) is an even function, we can study it only on \([0,\infty)\).

We have \[
f_n^\prime(x)= 2n^2x \frac{1-n^4x^4}{(1+n^4 x^4)^2}.\] \(f_n^\prime\) vanishes at zero (like \(f_n\)) is positive on \((0,\frac{1}{n})\), vanishes at \(\frac{1}{n}\) and is negative on \((\frac{1}{n},\infty)\). Hence \(f_n\) has a maximum at \(\frac{1}{n}\) with \(f_n(\frac{1}{n}) = \frac{1}{2}\) and \(0 \le f_n(x) \le \frac{1}{2}\) for all \(x \in \mathbb R\).

Also for \(x \neq 0\) \[
0 \le f_n(x) =\frac{n^2 x^2}{1+n^4 x^4} \le \frac{n^2 x^2}{n^4 x^4} = \frac{1}{n^2 x^2}\] consequently \[
0 \le f_n(x) \le \frac{1}{n} \text{ for } x \ge \frac{1}{\sqrt{n}}.\]

\((g_n)\) converges pointwise to zero

First, one can notice that \(g_n\) is well defined. For \(x \in \mathbb R\) and \(p \in \mathbb N\) we have \(0 \le \frac{1}{2^p} f_n(x-a_p) \le \frac{1}{2^p} \cdot\ \frac{1}{2}=\frac{1}{2^{p+1}}\) according to previous paragraph. Therefore the series of functions \(\sum \frac{1}{2^p} f_n(x-a_p)\) is normally convergent. \(g_n\) is also continuous as for all \(p \in \mathbb N\) \(x \mapsto \frac{1}{2^p} f_n(x-a_p)\) is continuous. Continue reading Pointwise convergence not uniform on any interval →