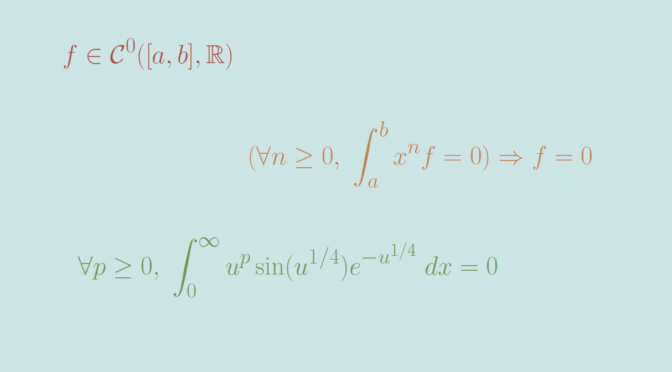Let’s consider the vector space \(\mathcal{C}^0([a,b],\mathbb R)\) of continuous real functions defined on a compact interval \([a,b]\). We can define an inner product on pairs of elements \(f,g\) of \(\mathcal{C}^0([a,b],\mathbb R)\) by \[
\langle f,g \rangle = \int_a^b f(x) g(x) \ dx.\]
It is known that \(f \in \mathcal{C}^0([a,b],\mathbb R)\) is the always vanishing function if we have \(\langle x^n,f \rangle = \int_a^b x^n f(x) \ dx = 0\) for all integers \(n \ge 0\). Let’s recall the proof. According to Stone-Weierstrass theorem, for all \(\epsilon >0\) it exists a polynomial \(P\) such that \(\Vert f – P \Vert_\infty \le \epsilon\). Then \[
\begin{aligned}
0 &\le \int_a^b f^2 = \int_a^b f(f-P) + \int_a^b fP\\
&= \int_a^b f(f-P) \le \Vert f \Vert_\infty \epsilon(b-a)
\end{aligned}\] As this is true for all \(\epsilon > 0\), we get \(\int_a^b f^2 = 0\) and \(f = 0\).
We now prove that the result becomes false if we change the interval \([a,b]\) into \([0, \infty)\), i.e. that one can find a continuous function \(f \in \mathcal{C}^0([0,\infty),\mathbb R)\) such that \(\int_0^\infty x^n f(x) \ dx\) for all integers \(n \ge 0\). In that direction, let’s consider the complex integral \[
I_n = \int_0^\infty x^n e^{-(1-i)x} \ dx.\] \(I_n\) is well defined as for \(x \in [0,\infty)\) we have \(\vert x^n e^{-(1-i)x} \vert = x^n e^{-x}\) and \(\int_0^\infty x^n e^{-x} \ dx\) converges. By integration by parts, one can prove that \[
I_n = \frac{n!}{(1-i)^{n+1}} = \frac{(1+i)^{n+1}}{2^{n+1}} n! = \frac{e^{i \frac{\pi}{4}(n+1)}}{2^{\frac{n+1}{2}}}n!.\] Consequently, \(I_{4p+3} \in \mathbb R\) for all \(p \ge 0\) which means \[
\int_0^\infty x^{4p+3} \sin(x) e^{-x} \ dx =0\] and finally \[
\int_0^\infty u^p \sin(u^{1/4}) e^{-u^{1/4}} \ dx =0\] for all integers \(p \ge 0\) using integration by substitution with \(x = u^{1/4}\). The function \(u \mapsto \sin(u^{1/4}) e^{-u^{1/4}}\) is one we were looking for.