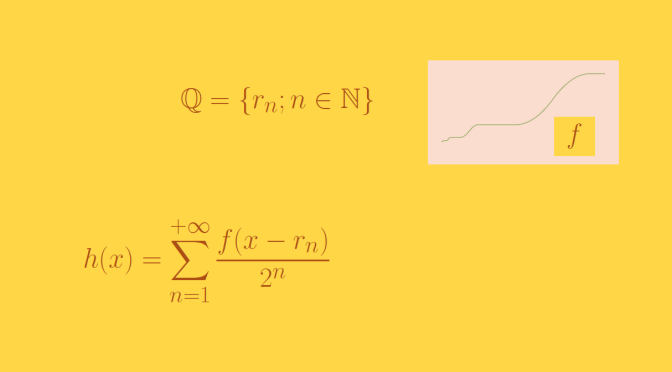Tag Archives: differentiability

Analysis

Converse of fundamental theorem of calculus

Leave a comment

The fundamental theorem of calculus asserts that for a continuous real-valued function \(f\) defined on a closed interval \([a,b]\), the function \(F\) defined for all \(x \in [a,b]\) by
\[F(x)=\int _{a}^{x}\!f(t)\,dt\] is uniformly continuous on \([a,b]\), differentiable on the open interval \((a,b)\) and \[
F^\prime(x) = f(x)\]
for all \(x \in (a,b)\).

The converse of fundamental theorem of calculus is not true as we see below.

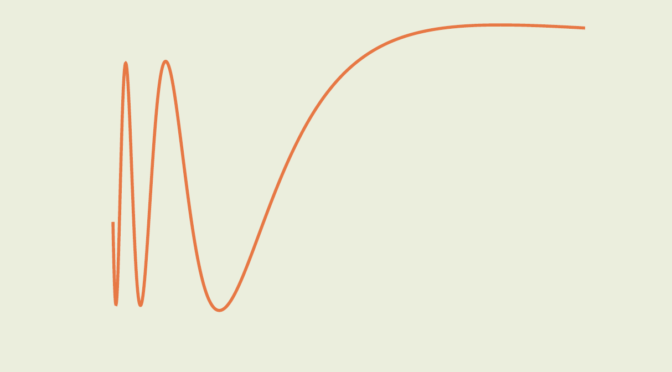
Consider the function defined on the interval \([0,1]\) by \[
f(x)= \begin{cases}
2x\sin(1/x) – \cos(1/x) & \text{ for } x \neq 0 \\
0 & \text{ for } x = 0 \end{cases}\] \(f\) is integrable as it is continuous on \((0,1]\) and bounded on \([0,1]\). Then \[
F(x)= \begin{cases}
x^2 \sin \left( 1/x \right) & \text{ for } x \neq 0 \\
0 & \text{ for } x = 0 \end{cases}\] \(F\) is differentiable on \([0,1]\). It is clear for \(x \in (0,1]\). \(F\) is also differentiable at \(0\) as for \(x \neq 0\) we have \[
\left\vert \frac{F(x) – F(0)}{x-0} \right\vert = \left\vert \frac{F(x)}{x} \right\vert \le \left\vert x \right\vert.\] Consequently \(F^\prime(0) = 0\).

However \(f\) is not continuous at \(0\) as it does not have a right limit at \(0\).

Analysis

A strictly increasing continuous function that is differentiable at no point of a null set

Leave a comment

We build in this article a strictly increasing continuous function \(f\) that is differentiable at no point of a null set \(E\). The null set \(E\) can be chosen arbitrarily. In particular it can have the cardinality of the continuum like the Cantor null set.

A set of strictly increasing continuous functions

For \(p \lt q\) two real numbers, consider the function \[
f_{p,q}(x)=(q-p) \left[\frac{\pi}{2} + \arctan{\left(\frac{2x-p-q}{q-p}\right)}\right]\] \(f_{p,q}\) is positive and its derivative is \[
f_{p,q}^\prime(x) = \frac{2}{1+\left(\frac{2x-p-q}{q-p}\right)^2}\] which is always strictly positive. Hence \(f_{p,q}\) is strictly increasing. We also have \[
\lim\limits_{x \to -\infty} f_{p,q}(x) = 0 \text{ and } \lim\limits_{x \to \infty} f_{p,q}(x) = \pi(q-p).\] One can notice that for \(x \in (p,q)\), \(f_{p,q}^\prime(x) \gt 1\). Therefore for \(x, y \in (p,q)\) distinct we have according to the mean value theorem \(\frac{f_{p,q}(y)-f_{p,q}(x)}{y-x} \ge 1\).

Covering \(E\) with an appropriate set of open intervals

As \(E\) is a null set, for each \(n \in \mathbb N\) one can find an open set \(O_n\) containing \(E\) and measuring less than \(2^{-n}\). \(O_n\) can be written as a countable union of disjoint open intervals as any open subset of the reals. Then \(I=\bigcup_{m \in \mathbb N} O_m\) is also a countable union of open intervals \(I_n\) with \(n \in \mathbb N\). The sum of the lengths of the \(I_n\) is less than \(1\). Continue reading A strictly increasing continuous function that is differentiable at no point of a null set →

Analysis

The Schwarz lantern

Leave a comment

Consider a smooth curve defined by a continuous map \(f : [0,1] \to \mathbb R^n\) with \(n \ge 2\) where \(f\) is supposed to have a continuous derivative. One can prove that the curve is rectifiable, its arc length being \[
L = \lim\limits_{n \to \infty} \sum_{i=1}^n \vert f(t_i) – f(t_{i-1}) \vert = \int_0^1 \vert f^\prime (t) \vert \ dt\] with \(t_i = \frac{i}{n}\) for \(0 \le i \le n\).

What can happen when we consider a surface instead of a curve?

Consider a compact, smooth surface (possibly with boundary) embedded in \(\mathbb R^3\). We can approximate it as a polyhedral surface composed of small triangles with all vertices on the initial surface. Will the sum of the areas of the triangles converges to the area of the surface if their size is converging to zero?

The answer is negative and we provide a counterexample named Schwarz lantern. We take a cylinder of radius \(r\) and height \(h\). We approximate the cylinder by \(4nm\) isosceles triangles positioned as in the picture in \(2n\) slices. All triangles have the same base and height given by \[
b = 2r \sin \left(\frac{\pi}{m}\right), \ h = \sqrt{r^2 \left[1-\cos \left(\frac{\pi}{m}\right)\right]^2+\left(\frac{h}{2n}\right)^2}\] Hence the area of the polyhedral surface is \[
\begin{aligned}
S^\prime(m,n) &= 4 m n r \sin \left(\frac{\pi}{m}\right) \sqrt{r^2 \left[1-\cos \left(\frac{\pi}{m}\right)\right]^2+\left(\frac{h}{2n}\right)^2}\\
&= 4 m n r \sin \left(\frac{\pi}{m}\right) \sqrt{4 r^2 \sin^4 \left(\frac{\pi}{2m} \right)+\left(\frac{h}{2n}\right)^2}
\end{aligned}\] From there, let’s have a look to the value of \(S^\prime(m,n)\) as \(m,n \to \infty\).

Continue reading The Schwarz lantern →

Analysis

Differentiability of multivariable real functions (part2)

Leave a comment

Following the article on differentiability of multivariable real functions (part 1), we look here at second derivatives. We consider a function \(f : \mathbb R^n \to \mathbb R\) with \(n \ge 2\).

Schwarz’s theorem states that if \(f : \mathbb R^n \to \mathbb R\) has continuous second partial derivatives at any given point in \(\mathbb R^n\), then for \((a_1, \dots, a_n) \in \mathbb R^n\) and \(i,j \in \{1, \dots, n\}\):
\[\frac{\partial^2 f}{\partial x_i \partial x_j}(a_1, \dots, a_n)=\frac{\partial^2 f}{\partial x_j \partial x_i}(a_1, \dots, a_n)\]

A function for which \(\frac{\partial^2 f}{\partial x \partial y}(0,0) \neq \frac{\partial^2 f}{\partial y \partial x}(0,0)\)

We consider:
\[\begin{array}{l|rcl}
f : & \mathbb R^2 & \longrightarrow & \mathbb R \\
& (0,0) & \longmapsto & 0\\
& (x,y) & \longmapsto & \frac{xy(x^2-y^2)}{x^2+y^2} \text{ for } (x,y) \neq (0,0)
\end{array}\] Continue reading Differentiability of multivariable real functions (part2) →

Analysis

Differentiability of multivariable real functions (part1)

2 Comments

This article provides counterexamples about differentiability of functions of several real variables. We focus on real functions of two real variables (defined on \(\mathbb R^2\)). \(\mathbb R^2\) and \(\mathbb R\) are equipped with their respective Euclidean norms denoted by \(\Vert \cdot \Vert\) and \(\vert \cdot \vert\), i.e. the absolute value for \(\mathbb R\).

We recall some definitions and theorems about differentiability of functions of several real variables.

Definition 1 We say that a function \(f : \mathbb R^2 \to \mathbb R\) is differentiable at \(\mathbf{a} \in \mathbb R^2\) if it exists a (continuous) linear map \(\nabla f(\mathbf{a}) : \mathbb R^2 \to \mathbb R\) with \[\lim\limits_{\mathbf{h} \to 0} \frac{f(\mathbf{a}+\mathbf{h})-f(\mathbf{a})-\nabla f(\mathbf{a}).\mathbf{h}}{\Vert \mathbf{h} \Vert} = 0\]

Definition 2 Let \(f : \mathbb R^n \to \mathbb R\) be a real-valued function. Then the \(\mathbf{i^{th}}\) partial derivative at point \(\mathbf{a}\) is the real number
\begin{align*}
\frac{\partial f}{\partial x_i}(\mathbf{a}) &= \lim\limits_{h \to 0} \frac{f(\mathbf{a}+h \mathbf{e_i})- f(\mathbf{a})}{h}\\
&= \lim\limits_{h \to 0} \frac{f(a_1,\dots,a_{i-1},a_i+h,a_{i+1},\dots,a_n) – f(a_1,\dots,a_{i-1},a_i,a_{i+1},\dots,a_n)}{h}
\end{align*} For two real variable functions, \(\frac{\partial f}{\partial x}(x,y)\) and \(\frac{\partial f}{\partial y}(x,y)\) will denote the partial derivatives.

Definition 3 Let \(f : \mathbb R^n \to \mathbb R\) be a real-valued function. The directional derivative of \(f\) along vector \(\mathbf{v}\) at point \(\mathbf{a}\) is the real \[\nabla_{\mathbf{v}}f(\mathbf{a}) = \lim\limits_{h \to 0} \frac{f(\mathbf{a}+h \mathbf{v})- f(\mathbf{a})}{h}\] Continue reading Differentiability of multivariable real functions (part1) →

Analysis

A continuous function not differentiable at the rationals but differentiable elsewhere

Leave a comment

We build here a continuous function of one real variable whose derivative exists on \(\mathbb{R} \setminus \mathbb{Q}\) and doesn’t have a left or right derivative on each point of \(\mathbb{Q}\).

As \(\mathbb{Q}\) is (infinitely) countable, we can find a bijection \(n \mapsto r_n\) from \(\mathbb{N}\) to \(\mathbb{Q}\). We now reuse the function \(f\) defined here. Recall \(f\) main properties: Continue reading A continuous function not differentiable at the rationals but differentiable elsewhere →

Analysis

A differentiable function except at one point with a bounded derivative

1 Comment

We build here a continuous function of one real variable whose derivative exists except at \(0\) and is bounded on \(\mathbb{R^*}\).

We start with the even and piecewise linear function \(g\) defined on \([0,+\infty)\) with following values:
\[g(x)=
\left\{
\begin{array}{ll}
0 & \mbox{if } x =0\\
0 & \mbox{if } x \in \{\frac{k}{4^n};(k,n) \in \{1,2,4\} \times \mathbb{N^*}\}\\
1 & \mbox{if } x \in \{\frac{3}{4^n};n \in \mathbb{N^*}\}\\
\end{array}
\right.
\]
The picture below gives an idea of the graph of \(g\) for positive values. Continue reading A differentiable function except at one point with a bounded derivative →

Analysis

A function that is everywhere continuous and nowhere differentiable

Leave a comment

Let \(f_1(x) = |x|\) for \(| x | \le \frac{1}{2}\), and let \(f_1\) be defined for other values of \(x\) by periodic continuation with period \(1\). \(f_1\) graph looks like following picture:
van-der-Waerden first function picture

\(f_1\) is continuous everywhere and differentiable on \(\mathbb{R} \setminus \mathbb{Z}\). Continue reading A function that is everywhere continuous and nowhere differentiable →