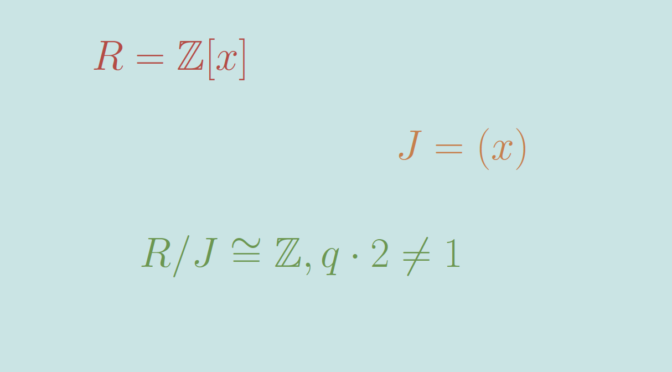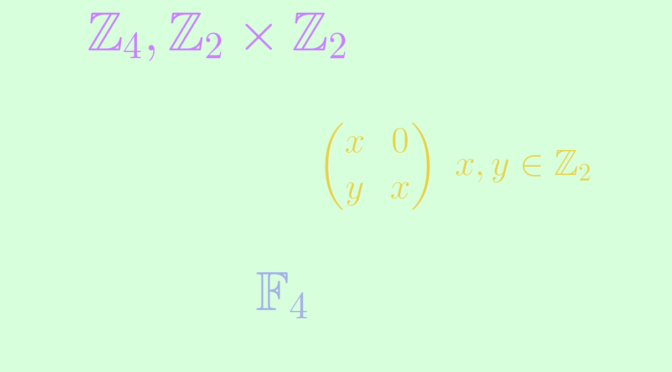Tag Archives: featured

Analysis

A semi-continuous function with a dense set of points of discontinuity

Leave a comment

Let’s come back to Thomae’s function which is defined as:
\[f:
\left|\begin{array}{lrl}
\mathbb{R} & \longrightarrow & \mathbb{R} \\
x & \longmapsto & 0 \text{ if } x \in \mathbb{R} \setminus \mathbb{Q} \\
\frac{p}{q} & \longmapsto & \frac{1}{q} \text{ if } \frac{p}{q} \text{ in lowest terms and } q > 0
\end{array}\right.\]

We proved here that \(f\) right-sided and left-sided limits vanish at all points. Therefore \(\limsup\limits_{x \to a} f(x) \le f(a)\) at every point \(a\) which proves that \(f\) is upper semi-continuous on \(\mathbb R\). However \(f\) is continuous at all \(a \in \mathbb R \setminus \mathbb Q\) and discontinuous at all \(a \in \mathbb Q\).

Algebra

A prime ideal that is not a maximal ideal

Leave a comment

Every maximal ideal is a prime ideal. The converse is true in a principal ideal domain – PID, i.e. every nonzero prime ideal is maximal in a PID, but this is not true in general. Let’s produce a counterexample.

\(R= \mathbb Z[x]\) is a ring. \(R\) is not a PID as can be shown considering the ideal \(I\) generated by the set \(\{2,x\}\). \(I\) cannot be generated by a single element \(p\). If it was, \(p\) would divide \(2\), i.e. \(p=1\) or \(p=2\). We can’t have \(p=1\) as it means \(R = I\) but \(3 \notin I\). We can’t have either \(p=2\) as it implies the contradiction \(x \notin I\). The ideal \(J = (x)\) is a prime ideal as \(R/J \cong \mathbb Z\) is an integral domain. Since \(\mathbb Z\) is not a field, \(J\) is not a maximal ideal.

Topology

Totally disconnected compact set with positive measure

1 Comment

Let’s build a totally disconnected compact set \(K \subset [0,1]\) such that \(\mu(K) >0\) where \(\mu\) denotes the Lebesgue measure.

In order to do so, let \(r_1, r_2, \dots\) be an enumeration of the rationals. To each rational \(r_i\) associate the open interval \(U_i = (r_i – 2^{-i-2}, r_i + 2^{-i-2})\). Then take \[
\displaystyle V = \bigcup_{i=1}^\infty U_i \text{ and } K = [0,1] \cap V^c.\] Clearly \(K\) is bounded and closed, therefore compact. As Lebesgue measure is subadditive we have \[
\mu(V) \le \sum_{i=1}^\infty \mu(U_i) \le \sum_{i=1}^\infty 2^{-i-1} = 1/2.\] This implies \[
\mu(K) = \mu([0,1]) – \mu([0,1] \cap V) \ge 1/2.\] In a further article, we’ll build a totally disconnected compact set \(K^\prime\) of \([0,1]\) with a predefined measure \(m \in [0,1)\).

Analysis

Converse of fundamental theorem of calculus

Leave a comment

The fundamental theorem of calculus asserts that for a continuous real-valued function \(f\) defined on a closed interval \([a,b]\), the function \(F\) defined for all \(x \in [a,b]\) by
\[F(x)=\int _{a}^{x}\!f(t)\,dt\] is uniformly continuous on \([a,b]\), differentiable on the open interval \((a,b)\) and \[
F^\prime(x) = f(x)\]
for all \(x \in (a,b)\).

The converse of fundamental theorem of calculus is not true as we see below.

Consider the function defined on the interval \([0,1]\) by \[
f(x)= \begin{cases}
2x\sin(1/x) – \cos(1/x) & \text{ for } x \neq 0 \\
0 & \text{ for } x = 0 \end{cases}\] \(f\) is integrable as it is continuous on \((0,1]\) and bounded on \([0,1]\). Then \[
F(x)= \begin{cases}
x^2 \sin \left( 1/x \right) & \text{ for } x \neq 0 \\
0 & \text{ for } x = 0 \end{cases}\] \(F\) is differentiable on \([0,1]\). It is clear for \(x \in (0,1]\). \(F\) is also differentiable at \(0\) as for \(x \neq 0\) we have \[
\left\vert \frac{F(x) – F(0)}{x-0} \right\vert = \left\vert \frac{F(x)}{x} \right\vert \le \left\vert x \right\vert.\] Consequently \(F^\prime(0) = 0\).

However \(f\) is not continuous at \(0\) as it does not have a right limit at \(0\).

Algebra

Four elements rings

Leave a comment

A group with four elements is isomorphic to either the cyclic group \(\mathbb Z_4\) or to the Klein four-group \(\mathbb Z_2 \times \mathbb Z_2\). Those groups are commutative. Endowed with the usual additive and multiplicative operations, \(\mathbb Z_4\) and \(\mathbb Z_2 \times \mathbb Z_2\) are commutative rings.

Are all four elements rings also isomorphic to either \(\mathbb Z_4\) or \(\mathbb Z_2 \times \mathbb Z_2\)? The answer is negative. Let’s provide two additional examples of commutative rings with four elements not isomorphic to \(\mathbb Z_4\) or \(\mathbb Z_2 \times \mathbb Z_2\).

The first one is the field \(\mathbb F_4\). \(\mathbb F_4\) is a commutative ring with four elements. It is not isomorphic to \(\mathbb Z_4\) or \(\mathbb Z_2 \times \mathbb Z_2\) as both of those rings have zero divisor. Indeed we have \(2 \cdot 2 = 0\) in \(\mathbb Z_4\) and \((1,0) \cdot (0,1)=(0,0)\) in \(\mathbb Z_2 \times \mathbb Z_2\).

A second one is the ring \(R\) of the matrices \(\begin{pmatrix}
x & 0\\
y & x\end{pmatrix}\) where \(x,y \in \mathbb Z_2\). One can easily verify that \(R\) is a commutative subring of the ring \(M_2(\mathbb Z_2)\). It is not isomorphic to \(\mathbb Z_4\) as its characteristic is \(2\). This is not isomorphic to \(\mathbb Z_2 \times \mathbb Z_2\) either as \(\begin{pmatrix}
0 & 0\\
1 & 0\end{pmatrix}\) is a non-zero matrix solution of the equation \(X^2=0\). \((0,0)\) is the only solution of that equation in \(\mathbb Z_2 \times \mathbb Z_2\).

One can prove that the four rings mentioned above are the only commutative rings with four elements up to isomorphism.

Analysis

Counterexamples around series (part 2)

Leave a comment

We follow the article counterexamples around series (part 1) providing additional funny series examples.

If \(\sum u_n\) converges and \((u_n)\) is non-increasing then \(u_n = o(1/n)\)?

This is true. Let’s prove it.
The hypotheses imply that \((u_n)\) converges to zero. Therefore \(u_n \ge 0\) for all \(n \in \mathbb N\). As \(\sum u_n\) converges we have \[
\displaystyle \lim\limits_{n \to \infty} \sum_{k=n/2}^{n} u_k = 0.\] Hence for \(\epsilon \gt 0\), one can find \(N \in \mathbb N\) such that \[
\epsilon \ge \sum_{k=n/2}^{n} u_k \ge \frac{1}{2} (n u_n) \ge 0\] for all \(n \ge N\). Which concludes the proof.

\(\sum u_n\) convergent is equivalent to \(\sum u_{2n}\) and \(\sum u_{2n+1}\) convergent?

Is not true as we can see taking \(u_n = \frac{(-1)^n}{n}\). \(\sum u_n\) converges according to the alternating series test. However for \(n \in \mathbb N\) \[
\sum_{k=1}^n u_{2k} = \sum_{k=1}^n \frac{1}{2k} = 1/2 \sum_{k=1}^n \frac{1}{k}.\] Hence \(\sum u_{2n}\) diverges as the harmonic series diverges.

\(\sum u_n\) absolutely convergent is equivalent to \(\sum u_{2n}\) and \(\sum u_{2n+1}\) absolutely convergent?

This is true and the proof is left to the reader.

\(\sum u_n\) is a positive convergent series then \((\sqrt[n]{u_n})\) is bounded?

Is true. If not, there would be a subsequence \((u_{\phi(n)})\) such that \(\sqrt[\phi(n)]{u_{\phi(n)}} \ge 2\). Which means \(u_{\phi(n)} \ge 2^{\phi(n)}\) for all \(n \in \mathbb N\) and implies that the sequence \((u_n)\) is unbounded. In contradiction with the convergence of the series \(\sum u_n\).

If \((u_n)\) is strictly positive with \(u_n = o(1/n)\) then \(\sum (-1)^n u_n\) converges?

It does not hold as we can see with \[
u_n=\begin{cases} \frac{1}{n \ln n} & n \equiv 0 [2] \\
\frac{1}{2^n} & n \equiv 1 [2] \end{cases}\] Then for \(n \in \mathbb N\) \[
\sum_{k=1}^{2n} (-1)^k u_k \ge \sum_{k=1}^n \frac{1}{2k \ln 2k} – \sum_{k=1}^{2n} \frac{1}{2^k} \ge \sum_{k=1}^n \frac{1}{2k \ln 2k} – 1.\] As \(\sum \frac{1}{2k \ln 2k}\) diverges as can be proven using the integral test with the function \(x \mapsto \frac{1}{2x \ln 2x}\), \(\sum (-1)^n u_n\) also diverges.