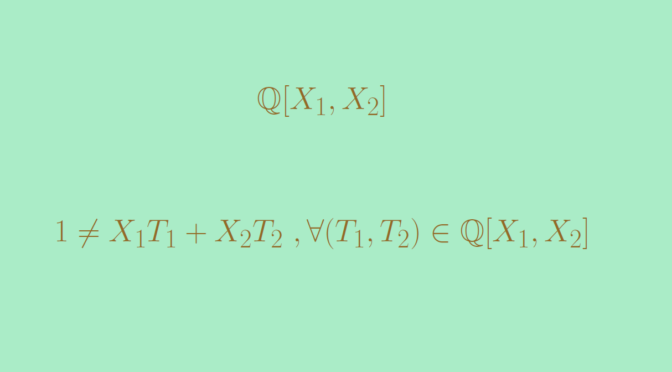Monthly Archives: April 2016

Algebra

Unique factorization domain that is not a Principal ideal domain

Leave a comment

In this article, we provide an example of a unique factorization domain – UFD that is not a principal ideal domain – PID. However, it is known that a PID is a UFD.

We take a field \(F\), for example \(\mathbb Q\), \(\mathbb R\), \(\mathbb F_p\) (where \(p\) is a prime) or whatever more exotic.

The polynomial ring \(F[X]\) is a UFD. This follows from the fact that \(F[X]\) is a Euclidean domain. It is also known that for a UFD \(R\), \(R[X]\) is also a UFD. Therefore the polynomial ring \(F[X_1,X_2]\) in two variables is a UFD as \(F[X_1,X_2] = F[X_1][X_2]\). However the ideal \(I=(X_1,X_2)\) is not principal. Let’s prove it by contradiction.

Suppose that \((X_1,X_2) = (P)\) with \(P \in F[X_1,X_2]\). Then there exist two polynomials \(Q_1,Q_2 \in F[X_1,X_2]\) such that \(X_1=PQ_1\) and \(X_2=PQ_2\). As a polynomial in variable \(X_2\), the polynomial \(X_1\) is having degree \(0\). Therefore, the degree of \(P\) as a polynomial in variable \(X_2\) is also equal to \(0\). By symmetry, we get that the degree of \(P\) as a polynomial in variable \(X_1\) is equal to \(0\) too. Which implies that \(P\) is an element of the field \(F\) and consequently that \((X_1,X_2) = F[X_1,X_2]\).

But the equality \((X_1,X_2) = F[X_1,X_2]\) is absurd. Indeed, the degree of a polynomial \(X_1 T_1 + X_2 T_2\) cannot be equal to \(0\) for any \(T_1,T_2 \in F[X_1,X_2]\). And therefore \(1 \notin F[X_1,X_2]\).

Set Theory

A non-measurable set

Leave a comment

We describe here a non-measurable subset of the segment \(I=[0,1] \subset \mathbb R\).

Let’s define on \(I\) an equivalence relation by \(x \sim y\) if and only if \(x-y \in \mathbb Q\). The equivalence relation \(\sim\) induces equivalence classes on \(I\). For \(x \in I\), it’s equivalence class \([x]\) is \([x] = \{y \in I \ : \ y-x \in \mathbb Q\}\). By the Axiom of Choice, we can form a set \(A\) by selecting a single point from each equivalence class.

We claim that the set \(A\) is not Lebesgue measurable.

For all \(q \in \mathbb Q\) we denote \(A_q = \{q+x \ : x \in A\}\). Let’s take \(p,q \in \mathbb Q\). If it exists \(z \in A_p \cap A_q\), it means that there exist \(u,v \in A\) such that
\[z= p+u=q+v\] hence \(u-v=q-p=0\) as \(u,v\) are supposed to be unique representatives of the classes of the equivalence relation \(\sim\). Finally if \(p,q\) are distincts, \(A_p \cap A_q = \emptyset\).

As Lebesgue measure \(\mu\) is translation invariant, we have for \(q \in \mathbb Q \cap [0,1]\) : \(\mu(A) = \mu(A_q)\) and also \(A_q \subset [0,2]\). Hence if we denote
\[B = \bigcup_{q \in \mathbb Q \cap [0,1]} A_q\] we have \(B \subset [0,2]\). If we suppose that \(A\) is measurable, we get
\[\mu(B) = \sum_{q \in \mathbb Q \cap [0,1]} \mu(A_q) = \sum_{q \in \mathbb Q \cap [0,1]} \mu(A) \le 2\] by countable additivity of Lebesgue measure (the set \(\mathbb Q \cap [0,1]\) being countable infinite). This implies \(\mu(A) = 0\).

Let’s prove now that
\[[0,1] \subset \bigcup_{q \in \mathbb Q \cap [-1,1]} A_q\] For \(z \in [0,1]\), there exists \(u \in A\) such that \(z \in [u]\). As \(A \subset [0,1]\), we have \(q = z-u \in \mathbb Q\) and \(-1 \le q \le 1\). And \(z=q+u\) means that \(z \in A_q\). This proves the inclusion. However the inclusion implies the contradiction
\[1 = \mu([0,1]) \le \sum_{q \in \mathbb Q \cap [-1,1]} \mu(A_q) = \sum_{q \in \mathbb Q \cap [-1,1]} \mu(A) =0\]

Finally \(A\) is not Lebesgue measurable.

Topology

Isometric versus affine

Leave a comment

Throughout this article we let \(E\) and \(F\) denote real normed vector spaces. A map \(f : E \rightarrow F\) is an isometry if \(\Vert f(x) – f(y) \Vert = \Vert x – y \Vert\) for all \(x, y \in E\), and \(f\) is affine if \[
f((1-t) a + t b ) = (1-t) f(a) + t f(b) \] for all \(a,b \in E\) and \(t \in [0,1]\). Equivalently, \(f\) is affine if the map \(T : E \rightarrow F\), defined by \(T(x)=f(x)-f(0)\) is linear.

First note that an isometry \(f\) is always one-to-one as \(f(x) = f(y)\) implies \[
0 = \Vert f(x) – f(y) \Vert = \Vert x- y \Vert\] hence \(x=y\).

There are two important cases when every isometry is affine:

  1. \(f\) is bijective (equivalently surjective). This is Mazur-Ulam theorem, which was proven in 1932.
  2. \(F\) is a strictly convex space. Recall that a normed vector space \((S, \Vert \cdot \Vert)\) is strictly convex if and only if for all distinct \(x,y \in S\), \(\Vert x \Vert = \Vert y \Vert =1\) implies \(\Vert \frac{x+y}{2} \Vert <1\). For example, an inner product space is strictly convex. The sequence spaces \(\ell_p\) for \(1 < p < \infty\) are also strictly convex.

Continue reading Isometric versus affine →

Analysis

Counterexample around Morera’s theorem

Leave a comment

Let’s recall Morera’s theorem.

Morera’s theorem Suppose that \(f\) is a continuous complex-valued function in a connected open set \(\Omega \subset \mathbb C\) such that
\[\int_{\partial \Delta} f(z) \ dz = 0\] for every closed triangle \(\Delta \subset \Omega \setminus \{p\}\) where \(p \in \Omega\). Then \(f\) is holomorphic in \(\Omega\).

Does the conclusion of Morera’s theorem still hold if \(f\) is supposed to be continuous only in \(\Omega \setminus \{p\}\)? The answer is negative and we provide a counterexample.

Let \(\Omega\) be the entire complex plane, \(f\) defined as follows
\[f(z)=\begin{cases}
\frac{1}{z^2} & \text{if } z \neq 0\\
0 & \text{otherwise}
\end{cases}\] and \(p\) the origin.

For \(a,b \in \Omega \setminus \{0\}\) we have
\[\begin{aligned}
\int_{[a,b]} f(z) \ dz &= \int_{[a,b]} \frac{dz}{z^2}\\
&= \int_0^1 \frac{b-a}{[a+t(b-a)]^2} \ dt\\
&=\left[ -\frac{1}{a+t(b-a)} \right]_0^1 = \frac{1}{a} – \frac{1}{b}
\end{aligned}\]

Hence for a triangle \(\Delta\) with vertices at \(a,b ,c \in \Omega \setminus \{0\}\):
\[\int_{\partial \Delta} f(z) \ dz = \left( \frac{1}{a} – \frac{1}{b} \right) + \left( \frac{1}{b} – \frac{1}{c} \right) + \left( \frac{1}{c} – \frac{1}{a} \right)=0\]

However, \(f\) is not holomorphic in \(\Omega\) as it is even not continuous at \(0\).