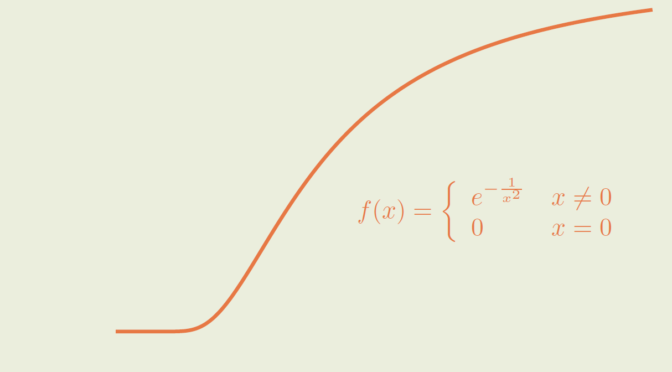Let’s consider the set \(\mathcal C^\infty(\mathbb R)\) of real smooth functions, i.e. functions that have derivatives of all orders on \(\mathbb R\).
Does a positive function \(f \in \mathcal C^\infty(\mathbb R)\) with all derivatives vanishing at zero exists?
Such a map \(f\) cannot be expandable in power series around zero, as it would vanish in a neighborhood of zero. However, the answer to our question is positive and we’ll prove that \[
f(x) = \left\{\begin{array}{lll}
e^{-\frac{1}{x^2}} &\text{if} &x \neq 0\\
0 &\text{if} &x = 0 \end{array}\right. \] provides an example.
\(f\) is well defined and positive for \(x \neq 0\). As \(\lim\limits_{x \to 0} -\frac{1}{x^2} = -\infty\), we get \(\lim\limits_{x \to 0} f(x) = 0\) proving that \(f\) is continuous on \(\mathbb R\). Let’s prove by induction that for \(x \neq 0\) and \(n \in \mathbb N\), \(f^{(n)}(x)\) can be written as \[
f^{(n)}(x) = \frac{P_n(x)}{x^{3n}}e^{-\frac{1}{x^2}}\] where \(P_n\) is a polynomial function. The statement is satisfied for \(n = 1\) as \(f^\prime(x) = \frac{2}{x^3}e^{-\frac{1}{x^2}}\). Suppose that the statement is true for \(n\) then \[
f^{(n+1)}(x)=\left[\frac{P_n^\prime(x)}{x^{3n}} – \frac{3n P_n(x)}{x^{3n+1}}+\frac{2 P_n(x)}{x^{3n+3}}\right] e^{-\frac{1}{x^2}}\] hence the statement is also true for \(n+1\) by taking \(P_{n+1}(x)=
x^3 P_n^\prime(x) – 3n x^2 P_n(x) + 2 P_n(x)\). Which concludes our induction proof.
Finally, we have to prove that for all \(n \in \mathbb N\), \(\lim\limits_{x \to 0} f^{(n)}(x) = 0\). For that, we use the power expansion of the exponential map \(e^x = \sum_{n=0}^\infty \frac{x^n}{n!}\). For \(x \neq 0\), we have \[
\left\vert x \right\vert^{3n} e^{\frac{1}{x^2}} \ge \frac{\vert x \vert^{3n}}{(2n)! \vert x \vert ^{4n}} = \frac{1}{(2n)! \vert x \vert^n}\] Therefore \(\lim\limits_{x \to 0} \left\vert x \right\vert^{3n} e^{\frac{1}{x^2}} = \infty\) and \(\lim\limits_{x \to 0} f^{(n)}(x) = 0\) as \(f^{(n)}(x) = \frac{P_n(x)}{x^{3n} e^{\frac{1}{x^2}}}\) with \(P_n\) a polynomial function.