Let’s build a totally disconnected compact set \(K \subset [0,1]\) such that \(\mu(K) >0\) where \(\mu\) denotes the Lebesgue measure.
In order to do so, let \(r_1, r_2, \dots\) be an enumeration of the rationals. To each rational \(r_i\) associate the open interval \(U_i = (r_i – 2^{-i-2}, r_i + 2^{-i-2})\). Then take \[
\displaystyle V = \bigcup_{i=1}^\infty U_i \text{ and } K = [0,1] \cap V^c.\] Clearly \(K\) is bounded and closed, therefore compact. As Lebesgue measure is subadditive we have \[
\mu(V) \le \sum_{i=1}^\infty \mu(U_i) \le \sum_{i=1}^\infty 2^{-i-1} = 1/2.\] This implies \[
\mu(K) = \mu([0,1]) – \mu([0,1] \cap V) \ge 1/2.\] In a further article, we’ll build a totally disconnected compact set \(K^\prime\) of \([0,1]\) with a predefined measure \(m \in [0,1)\).

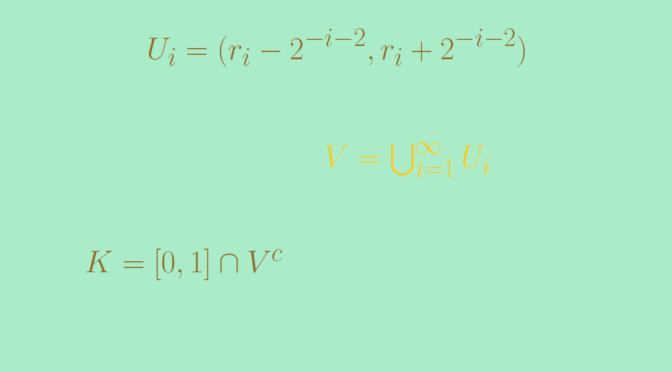
One thought on “Totally disconnected compact set with positive measure”