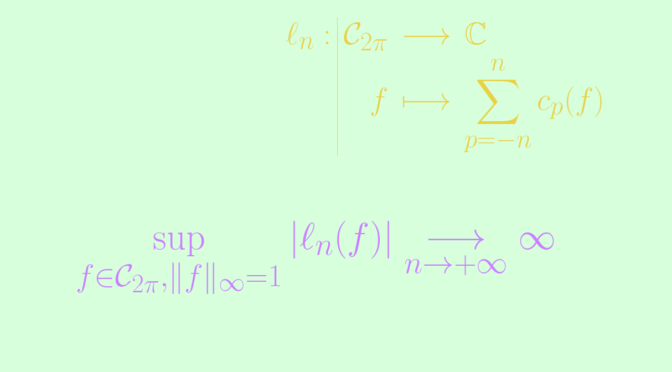Monthly Archives: October 2016

Analysis

Existence of a continuous function with divergent Fourier series

1 Comment

In that article, I provided an example of a continuous function with divergent Fourier series. We prove here the existence of such a function using Banach-Steinhaus theorem, also called uniform boundedness principle.

Theorem (Uniform Boundedness Theorem) Let \((X, \Vert \cdot \Vert_X)\) be a Banach space and \((Y, \Vert \cdot \Vert_Y)\) be a normed vector space. Suppose that \(F\) is a set of continuous linear operators from \(X\) to \(Y\). If for all \(x \in X\) one has \[
\sup\limits_{T \in F} \Vert T(x) \Vert_Y \lt \infty\] then \[
\sup\limits_{T \in F, \ \Vert x \Vert = 1} \Vert T(x) \Vert_Y \lt \infty\]

Let’s take for \(X\) the vector space \(\mathcal C_{2 \pi}\) of continuous functions from \(\mathbb R\) to \(\mathbb C\) which are periodic with period \(2 \pi\) endowed with the norm \(\Vert f \Vert_\infty = \sup\limits_{- \pi \le t \le \pi} \vert f(t) \vert\). \((\mathcal C_{2 \pi}, \Vert \cdot \Vert_\infty)\) is a Banach space. For the vector space \(Y\), we take the complex numbers \(\mathbb C\) endowed with the modulus.

For \(n \in \mathbb N\), the map \[
\begin{array}{l|rcl}
\ell_n : & \mathcal C_{2 \pi} & \longrightarrow & \mathbb C \\
& f & \longmapsto & \displaystyle \sum_{p=-n}^n c_p(f) \end{array}\] is a linear operator, where for \(p \in \mathbb Z\), \(c_p(f)\) denotes the complex Fourier coefficient \[
c_p(f) = \frac{1}{2 \pi} \int_{- \pi}^{\pi} f(t) e^{-i p t} \ dt\]

We now prove that
\begin{align*}
\Lambda_n &= \sup\limits_{f \in \mathcal C_{2 \pi}, \Vert f \Vert_\infty=1} \vert \ell_n(f) \vert\\
&= \frac{1}{2 \pi} \int_{- \pi}^{\pi} \left\vert \frac{\sin (2n+1)\frac{t}{2}}{\sin \frac{t}{2}} \right\vert \ dt = \frac{1}{2 \pi} \int_{- \pi}^{\pi} \left\vert h_n(t) \right\vert \ dt,
\end{align*} where one can notice that the function \[
\begin{array}{l|rcll}
h_n : & [- \pi, \pi] & \longrightarrow & \mathbb C \\
& t & \longmapsto & \frac{\sin (2n+1)\frac{t}{2}}{\sin \frac{t}{2}} &\text{for } t \neq 0\\
& 0 & \longmapsto & 2n+1
\end{array}\] is continuous.
Continue reading Existence of a continuous function with divergent Fourier series →

Analysis

A positive smooth function with all derivatives vanishing at zero

Leave a comment

Let’s consider the set \(\mathcal C^\infty(\mathbb R)\) of real smooth functions, i.e. functions that have derivatives of all orders on \(\mathbb R\).

Does a positive function \(f \in \mathcal C^\infty(\mathbb R)\) with all derivatives vanishing at zero exists?

Such a map \(f\) cannot be expandable in power series around zero, as it would vanish in a neighborhood of zero. However, the answer to our question is positive and we’ll prove that \[
f(x) = \left\{\begin{array}{lll}
e^{-\frac{1}{x^2}} &\text{if} &x \neq 0\\
0 &\text{if} &x = 0 \end{array}\right. \] provides an example.

\(f\) is well defined and positive for \(x \neq 0\). As \(\lim\limits_{x \to 0} -\frac{1}{x^2} = -\infty\), we get \(\lim\limits_{x \to 0} f(x) = 0\) proving that \(f\) is continuous on \(\mathbb R\). Let’s prove by induction that for \(x \neq 0\) and \(n \in \mathbb N\), \(f^{(n)}(x)\) can be written as \[
f^{(n)}(x) = \frac{P_n(x)}{x^{3n}}e^{-\frac{1}{x^2}}\] where \(P_n\) is a polynomial function. The statement is satisfied for \(n = 1\) as \(f^\prime(x) = \frac{2}{x^3}e^{-\frac{1}{x^2}}\). Suppose that the statement is true for \(n\) then \[
f^{(n+1)}(x)=\left[\frac{P_n^\prime(x)}{x^{3n}} – \frac{3n P_n(x)}{x^{3n+1}}+\frac{2 P_n(x)}{x^{3n+3}}\right] e^{-\frac{1}{x^2}}\] hence the statement is also true for \(n+1\) by taking \(P_{n+1}(x)=
x^3 P_n^\prime(x) – 3n x^2 P_n(x) + 2 P_n(x)\). Which concludes our induction proof.

Finally, we have to prove that for all \(n \in \mathbb N\), \(\lim\limits_{x \to 0} f^{(n)}(x) = 0\). For that, we use the power expansion of the exponential map \(e^x = \sum_{n=0}^\infty \frac{x^n}{n!}\). For \(x \neq 0\), we have \[
\left\vert x \right\vert^{3n} e^{\frac{1}{x^2}} \ge \frac{\vert x \vert^{3n}}{(2n)! \vert x \vert ^{4n}} = \frac{1}{(2n)! \vert x \vert^n}\] Therefore \(\lim\limits_{x \to 0} \left\vert x \right\vert^{3n} e^{\frac{1}{x^2}} = \infty\) and \(\lim\limits_{x \to 0} f^{(n)}(x) = 0\) as \(f^{(n)}(x) = \frac{P_n(x)}{x^{3n} e^{\frac{1}{x^2}}}\) with \(P_n\) a polynomial function.

Algebra

Non commutative rings

Leave a comment

Let’s recall that a set \(R\) equipped with two operations \((R,+,\cdot)\) is a ring if and only if \((R,+)\) is an abelian group, multiplication \(\cdot\) is associative and has a multiplicative identity \(1\) and multiplication is left and right distributive with respect to addition.

\((\mathbb Z, +, \cdot)\) is a well known infinite ring which is commutative. The rational, real and complex numbers are other infinite commutative rings. Those are in fact fields as every non-zero element have a multiplicative inverse.

For a field \(F\) (finite or infinite), the polynomial ring \(F[X]\) is another example of infinite commutative ring.

Also for \(n\) integer, the integers modulo n is a finite ring that is commutative. Finally, according to Wedderburn theorem every finite division ring is commutative.

So what are examples of non commutative rings? Let’s provide a couple. Continue reading Non commutative rings →

Set Theory

Around bounded sets, greatest element and supremum

Leave a comment

Consider a linearly ordered set \((X, \le)\) and a subset \(S \subseteq X\). Let’s recall some definitions:

  • \(S\) is bounded above if there exists an element \(k \in X\) such that \(k \ge s\) for all \(s \in S\).
  • \(g\) is a greatest element of \(S\) is \(g \in S\) and \(g \ge s\) for all \(s \in S\). \(l\) is a lowest element of \(S\) is \(l \in S\) and \(l \le s\) for all \(s \in S\).
  • \(a\) is an supremum of \(S\) if it is the least element in \(X\) that is greater than or equal to all elements of \(S\).

Subsets with a supremum but no greatest element

Let’s give examples of subsets having a supremum but no greatest element. First consider the ordered set \((\mathbb R, \le)\) and the subset \(S=\{ q \in \mathbb Q \ ; \ q \le \sqrt{2}\}\). \(S\) is bounded above by \(2\). \(\sqrt{2}\) is a supremum of \(S\) as we have \(q \le \sqrt{2}\) for all \(q \in S\) and as for \(b < \sqrt{2}\), it exists \(q \in \mathbb Q\) such that \(b < q < \sqrt{2}\) because \(\mathbb Q\) is dense in \(\mathbb R\). However \(S\) doesn't have a greatest element because \(\sqrt{2}\) is an irrational number.

For our second example we take \(X = \mathbb N \times \mathbb N\) ordered lexicographically by \(\preceq\). The subset \(S=\{(0,n) \ ; \ n \in \mathbb N\}\) is bounded above by \((2,0)\). Moreover \((1,0)\) is a supremum. But \(S\) doesn’t have a greatest element as for \((0,n) \in S\) we have \((0,n) \prec (0,n+1)\).

Bounded above subsets with no supremum

Leveraging the examples above, we take \((X, \le) = (\mathbb Q, \le)\) and \(S=\{ q \in \mathbb Q \ ; \ q \le \sqrt{2}\}\). \(S\) is bounded above, by \(2\) for example. However \(S\) doesn’t have a supremum because \(\sqrt{2} \notin \mathbb Q\).

Another example is the set \(X = \mathbb N \times \mathbb Z\) ordered lexicographically by \(\preceq\). The subset \(S=\{(0,n) \ ; \ n \in \mathbb N\}\) is bounded above by \((2,0)\) but has no supremum. Indeed, the elements greater or equal to all the elements of \(S\) are the elements \((a,b)\) with \(a \ge 1\). However \((a,b)\) with \(a \ge 1\) cannot be a supremum of \(S\), as \((a,b-1) \prec (a,b)\) and \((a,b-1)\) is greater than all the elements of \(S\).

Analysis

Counterexample around infinite products

Leave a comment

Let’s recall two theorems about infinite products \(\prod \ (1+a_n)\). The first one deals with nonnegative terms \(a_n\).

THEOREM 1 An infinite product \(\prod \ (1+a_n)\) with nonnegative terms \(a_n\) converges if and only if the series \(\sum a_n\) converges.

The second is related to infinite products with complex terms.

THEOREM 2 The absolute convergence of the series \(\sum a_n\) implies the convergence of the infinite product \(\prod \ (1+a_n)\). Moreover \(\prod \ (1+a_n)\) is not zero providing \(a_n \neq -1\) for all \(n \in \mathbb N\).

The converse of Theorem 2 is not true as shown by following counterexample.

We consider \(a_n=(-1)^n/(n+1)\). For \(N \in \mathbb N\) we have:
\[\prod_{n=1}^N \ (1+a_n) =
\begin{cases}
\frac{1}{2} &\text{ for } N \text{ odd}\\
\frac{1}{2}(1+\frac{1}{N+1}) &\text{ for } N \text{ even}
\end{cases}
\] hence the infinite product \(\prod \ (1+a_n)\) converges (to \(\frac{1}{2}\)) while the series \(\sum \left\vert a_n \right\vert = \sum \frac{1}{n+1}\) diverges (it is the harmonic series with first term omitted).