It is known that for a piecewise continuously differentiable function \(f\), the Fourier series of \(f\) converges at all \(x \in \mathbb R\) to \(\frac{f(x^-)+f(x^+)}{2}\).
We describe Fejér example of a continuous function with divergent Fourier series. Fejér example is the even, \((2 \pi)\)-periodic function \(f\) defined on \([0,\pi]\) by: \[
f(x) = \sum_{p=1}^\infty \frac{1}{p^2} \sin \left[ (2^{p^3} + 1) \frac{x}{2} \right]\]
According to Weierstrass M-test, \(f\) is continuous. We denote \(f\) Fourier series by \[
\frac{1}{2} a_0 + (a_1 \cos x + b_1 \sin x) + \dots + (a_n \cos nx + b_n \sin nx) + \dots.\]
As \(f\) is even, the \(b_n\) are all vanishing. If we denote for all \(m \in \mathbb N\):\[
\lambda_{n,m}=\int_0^{\pi} \sin \left[ (2m + 1) \frac{t}{2} \right] \cos nt \ dt \text{ and } \sigma_{n,m} = \sum_{k=0}^n \lambda_{k,m},\]
we have:\[
\begin{aligned}
a_n &=\frac{1}{\pi} \int_{-\pi}^{\pi} f(t) \cos nt \ dt= \frac{2}{\pi} \int_0^{\pi} f(t) \cos nt \ dt\\
&= \frac{2}{\pi} \int_0^{\pi} \left(\sum_{p=1}^\infty \frac{1}{p^2} \sin \left[ (2^{p^3} + 1) \frac{x}{2} \right]\right) \cos nt \ dt\\
&=\frac{2}{\pi} \sum_{p=1}^\infty \frac{1}{p^2} \int_0^{\pi} \sin \left[ (2^{p^3} + 1) \frac{x}{2} \right] \cos nt \ dt\\
&=\frac{2}{\pi} \sum_{p=1}^\infty \frac{1}{p^2} \lambda_{n,2^{p^3-1}}
\end{aligned}\] One can switch the \(\int\) and \(\sum\) signs as the series is normally convergent.
We now introduce for all \(n \in \mathbb N\):\[
S_n = \frac{\pi}{2} \sum_{k=0}^n a_k = \sum_{p=1}^\infty \sum_{k=0}^n \frac{1}{p^2} \lambda_{k,2^{p^3-1}}
=\sum_{p=1}^\infty \frac{1}{p^2} \sigma_{n,2^{p^3-1}}\]
We will prove below that for all \(n,m \in \mathbb N\) we have \(\sigma_{m,m} \ge \frac{1}{2} \ln m\) and \(\sigma_{n,m} \ge 0\). Assuming those inequalities for now, we get:\[
S_{2^{p^3-1}} \ge \frac{1}{p^2} \sigma_{2^{p^3-1},2^{p^3-1}} \ge \frac{1}{2p^2} \ln(2^{p^3-1}) = \frac{p^3-1}{2p^2} \ln 2\]
As the right hand side diverges to \(\infty\), we can conclude that \((S_n)\) diverges and consequently that the Fourier series of \(f\) diverges at \(0\).
Let’s now prove the inequalities we admitted above. Using the trigonometric formulae for the product of sinus and cosinus, we have \[
\begin{aligned}
\lambda_{n,m} &=\frac{1}{2} \int_0^{\pi} \left[\sin\left(\frac{2m+1}{2}+n\right) t + \sin\left(\frac{2m+1}{2}-n\right) t \right] \ dt\\
&=\frac{1}{2} \left(\frac{1}{m+n+1/2}+\frac{1}{m-n+1/2}\right) = \frac{m+1/2}{(m+1/2)^2-n^2}
\end{aligned}\] Therefore for \(n \le m\) we get \(\lambda_{n,m} \ge 0\) and \(\sigma_{q,m} \ge 0\) for \(q \le m\).
While for \(q \ge m\): \[
\begin{aligned}
2 \sigma_{q,m} &= \sum_{k=0}^q \left(\frac{1}{m+k+1/2}+\frac{1}{m-k+1/2}\right)\\
&=\sum_{i=m}^{q+m} \frac{1}{i+1/2} + \sum_{i=m}^{m-q} \frac{1}{i+1/2}\\
&= \sum_{i=m}^{q+m} \frac{1}{i+1/2} + \frac{1}{m+1/2} + \sum_{i=m-q}^{m-1} \frac{1}{i+1/2}\\
&= \frac{1}{m+1/2} + \sum_{i=q-m}^{q+m} \frac{1}{i+1/2} \ge 0
\end{aligned}\]
Hence for \(q=m\):\[
\begin{aligned}
2 \sigma_{m,m} &= \frac{1}{m+1/2} + \sum_{i=0}^{2m} \frac{1}{i+1/2}\\
&\ge \sum_{i=0}^{2m} \int_{i+1/2}^{i+3/2} \frac{dt}{t} = \int_{1/2}^{2m+3/2} \frac{dt}{t}\\
&= \ln(4m+3) \ge \ln m
\end{aligned}\] Proving as desired that \(\sigma_{m,m} \ge \frac{1}{2} \ln m\).

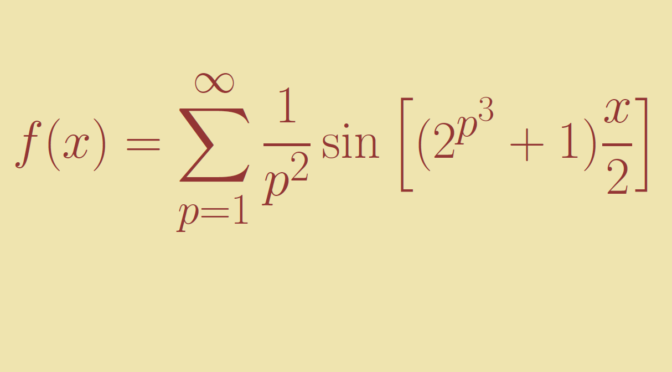
One thought on “A continuous function with divergent Fourier series”