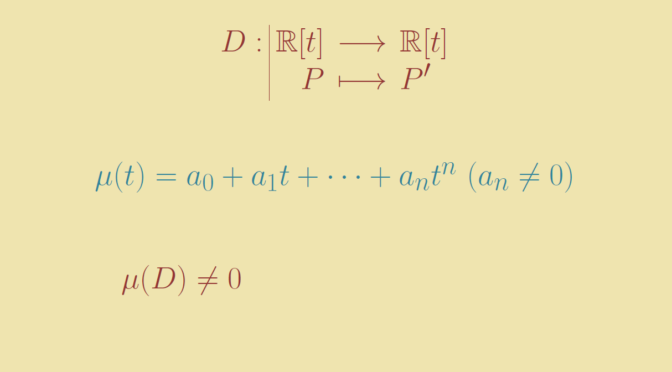Given an endomorphism \(T\) on a finite-dimensional vector space \(V\) over a field \(\mathbb F\), the minimal polynomial \(\mu_T\) of \(T\) is well defined as the generator (unique up to units in \(\mathbb F\)) of the ideal:\[
I_T= \{p \in \mathbb F[t]\ ; \ p(T)=0\}.\]

For infinite-dimensional vector spaces, the minimal polynomial might not be defined. Let’s provide an example.

We take the real polynomials \(V = \mathbb R [t]\) as a real vector space and consider the derivative map \(D : P \mapsto P^\prime\). Let’s prove that \(D\) doesn’t have any minimal polynomial. By contradiction, suppose that \[
\mu_D(t) = a_0 + a_1 t + \dots + a_n t^n \text{ with } a_n \neq 0\] is the minimal polynomial of \(D\), which means that for all \(P \in \mathbb R[t]\) we have \[
a_0 + a_1 P^\prime + \dots + a_n P^{(n)} = 0.\] Taking for \(P\) the polynomial \(t^n\) we get \[
a_0 t^n + n a_1 t^{n-1} + \dots + n! a_n = 0,\] which doesn’t make sense as \(n! a_n \neq 0\), hence \(a_0 t^n + n a_1 t^{n-1} + \dots + n! a_n\) cannot be the zero polynomial.

We conclude that \(D\) doesn’t have any minimal polynomial.

Consider a square matrix \(A\) of dimension \(n \ge 1\) over a field \(\mathbb F\), i.e. \(A \in \mathcal M_n(\mathbb F)\). Results discuss below are true for any field \(\mathbb F\), in particular for \(\mathbb F = \mathbb R\) or \(\mathbb F = \mathbb C\).

A polynomial \(P \in \mathbb F[X]\) is called a vanishing polynomial for \(A\) if \(P(A) = 0\). If the matrix \(B\) is similar to \(B\) (which means that \(B=Q^{-1} A Q\) for some invertible matrix \(Q\)), and the polynomial \(P\) vanishes at \(A\) then \(P\) also vanishes at \(B\). This is easy to prove as we have \(P(B)=P(Q^{-1} A Q)=Q^{-1} P(A) Q\).

In particular, two similar matrices have the same minimal and characteristic polynomials.

Is the converse true? Are two matrices having the same minimal and characteristic polynomials similar? Continue reading Two non similar matrices having same minimal and characteristic polynomials →