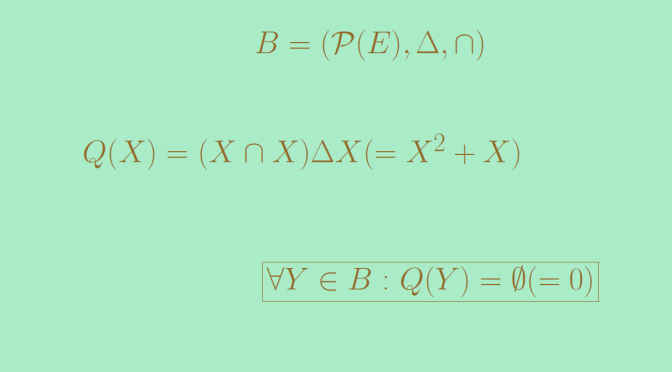Let’s consider a polynomial of degree \(q \ge 1\) over a field \(K\). It is well known that the sum of the multiplicities of the roots of \(P\) is less or equal to \(q\).
The result remains for polynomials over an integral domain. What is happening for polynomials over a commutative ring?
A polynomial of degree 2 having 4 roots
In this counterexample, we take for \(A=\mathbb{Z}/12\mathbb{Z}\) the quotient ring of integers modulo \(12\) and consider the polynomial \(P(X) = X^2 -4\).
Obviously \(x_1=2\) and \(x_2=-2=10\) are roots of \(P\). However that’s not the only ones! In particular, we also have:
- \(P(8)=64-4=5 \cdot 12=0\)
- \(P(10)=100-4=8 \cdot 12=0\)
So \(x_3=8\) and \(x_4=10\) are two other roots of \(P\).
As expected through the introduction of the topic, \(A=\mathbb{Z}/12\mathbb{Z}\) is not entire: \(3 \cdot 4 = 12 = 0\) in \(A\).
We also notice that \(P\) has several factorizations. In particular:
\[P(X)=X^2-4=(X-2)(X-10)=(X-8)(X-10)\]
A polynomial of degree 2 having an infinite number of roots
For this counterexample, let’s pick-up an infinite set \(E\) and consider the power set \(B=\mathcal{P}(E)\). On \(B\), we can define two operations. The first one \(\Delta\) is the symmetric difference and the second one \(\cap\) is the intersection.
\((B,\Delta, \cap)\) is a commutative ring. The proof is left to the reader. The empty set \(\emptyset\) is the unit element for \(\Delta\) (our ring addition) while \(E\) is the unit element for \(\cap\) (our ring multiplication). \(B\) is not entire as we can see by considering an element \(e \in E\) and the subsets \(R=\{e\}\) and \(\displaystyle S=\overline{\{e\}}\): we have \(R \cap S= \emptyset\).
We now look at the polynomial:
\[Q(X) = (X \cap X) \Delta X\]
\(Q(X)\) would just be \(X^2+X\) if we would have write \(\Delta\) as \(+\) and \(\cap\) as \(\times\).
Now for all \(T \in B=\mathcal{P}(E)\) we have \(T \cap T = T\) and \(T \Delta T = \emptyset\). Hence all elements of \(B\) are roots of \(Q\). However \(Q\) is not the zero polynomial.