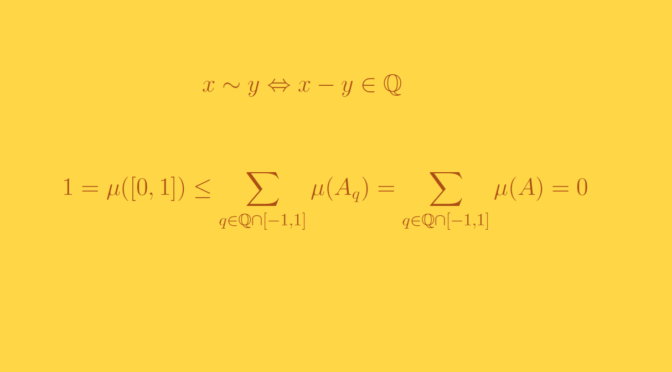We describe here a non-measurable subset of the segment $I=[0,1] \subset \mathbb R$.

Let’s define on $I$ an equivalence relation by $x \sim y$ if and only if $x-y \in \mathbb Q$. The equivalence relation $\sim$ induces equivalence classes on $I$. For $x \in I$, it’s equivalence class $[x]$ is $[x] = \{y \in I \ : \ y-x \in \mathbb Q\}$. By the Axiom of Choice, we can form a set $A$ by selecting a single point from each equivalence class.

We claim that the set $A$ is not Lebesgue measurable.

For all $q \in \mathbb Q$ we denote $A_q = \{q+x \ : x \in A\}$. Let’s take $p,q \in \mathbb Q$. If it exists $z \in A_p \cap A_q$, it means that there exist $u,v \in A$ such that
$$z= p+u=q+v$$ hence $u-v=q-p=0$ as $u,v$ are supposed to be unique representatives of the classes of the equivalence relation $\sim$. Finally if $p,q$ are distincts, $A_p \cap A_q = \emptyset$.

As Lebesgue measure $\mu$ is translation invariant, we have for $q \in \mathbb Q \cap [0,1]$ : $\mu(A) = \mu(A_q)$ and also $A_q \subset [0,2]$. Hence if we denote
$$B = \bigcup_{q \in \mathbb Q \cap [0,1]} A_q$$ we have $B \subset [0,2]$. If we suppose that $A$ is measurable, we get
$$\mu(B) = \sum_{q \in \mathbb Q \cap [0,1]} \mu(A_q) = \sum_{q \in \mathbb Q \cap [0,1]} \mu(A) \le 2$$ by countable additivity of Lebesgue measure (the set $\mathbb Q \cap [0,1]$ being countable infinite). This implies $\mu(A) = 0$.

Let’s prove now that
$$[0,1] \subset \bigcup_{q \in \mathbb Q \cap [-1,1]} A_q$$ For $z \in [0,1]$, there exists $u \in A$ such that $z \in [u]$. As $A \subset [0,1]$, we have $q = z-u \in \mathbb Q$ and $-1 \le q \le 1$. And $z=q+u$ means that $z \in A_q$. This proves the inclusion. However the inclusion implies the contradiction
$$1 = \mu([0,1]) \le \sum_{q \in \mathbb Q \cap [-1,1]} \mu(A_q) = \sum_{q \in \mathbb Q \cap [-1,1]} \mu(A) =0$$

Finally $A$ is not Lebesgue measurable.