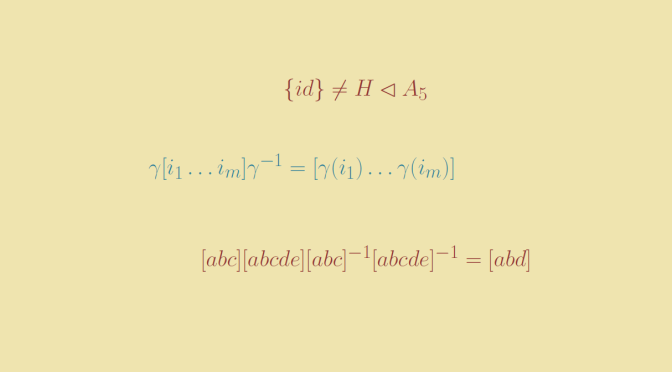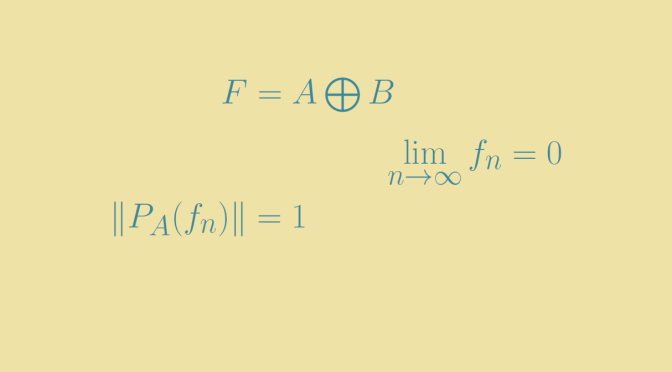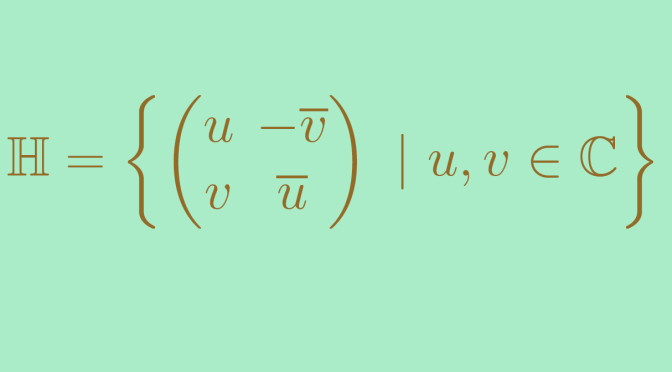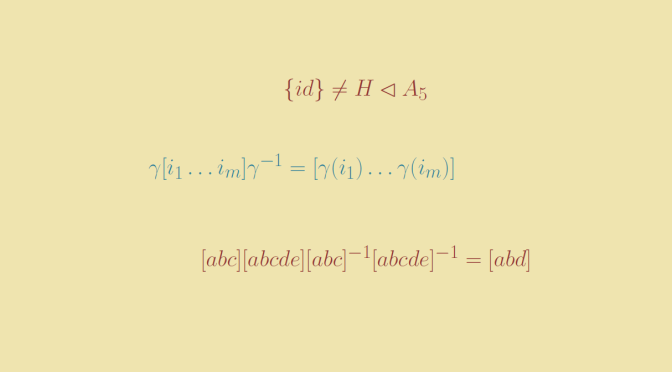
Consider a finite group \(G\) whose order (number of elements) is a prime number. It is well known that \(G\) is cyclic and simple. Which means that \(G\) has no non trivial normal subgroup.
Is the converse true, i.e. are the cyclic groups with prime orders the only simple groups? The answer is negative. We prove here that for \(n \ge 5\) the alternating group \(A_n\) is simple. In particular \(A_5\) whose order is equal to \(60\) is simple. Continue reading A simple group whose order is not a prime →
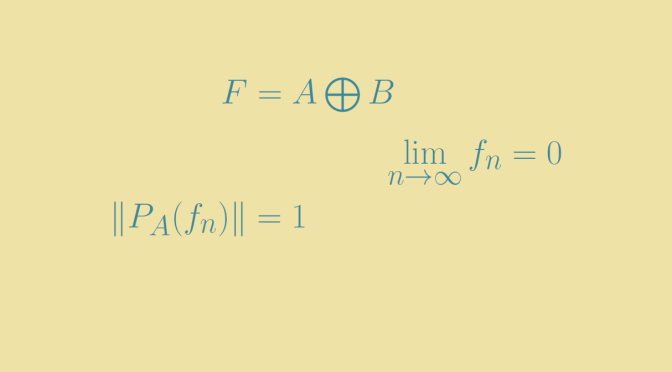
We give here an example of a two complemented subspaces \(A\) and \(B\) that are not topologically complemented.
For this, we consider a vector space of infinite dimension equipped with an inner product. We also suppose that \(E\) is separable. Hence, \(E\) has an orthonormal basis \((e_n)_{n \in \mathbb N}\).
Let \(a_n=e_{2n}\) and \(b_n=e_{2n}+\frac{1}{2n+1} e_{2n+1}\). We denote \(A\) and \(B\) the closures of the linear subspaces generated by the vectors \((a_n)\) and \((b_n)\) respectively. We consider \(F=A+B\) and prove that \(A\) and \(B\) are complemented subspaces in \(F\), but not topologically complemented. Continue reading Two algebraically complemented subspaces that are not topologically complemented →

Let \(f\) and \(g\) be two real functions and \(a \in \mathbb R \cup \{+\infty\}\). We provide here examples and counterexamples regarding the limits of \(f\) and \(g\).
If \(f\) has a limit as \(x\) tends to \(a\) then \(\vert f \vert\) also?
This is true. It is a consequence of the reverse triangle inequality \[\left\vert \vert f(x) \vert – \vert l \vert \right\vert \le \vert f(x) – l \vert\] Hence if \(\displaystyle \lim\limits_{x \to a} f(x) = l\), \(\displaystyle \lim\limits_{x \to a} \vert f(x) \vert = \vert l \vert\)
Is the converse of previous statement also true?
It is not. Consider the function defined by: \[\begin{array}{l|rcl}
f : & \mathbb R & \longrightarrow & \mathbb R \\
& \frac{1}{n} & \longmapsto & -1 \text{ for } n \ge 1 \text{ integer} \\
& x & \longmapsto & 1 \text{ otherwise} \end{array}\] \(\vert f \vert\) is the constant function equal to \(1\), hence \(\vert f \vert\) has \(1\) for limit as \(x\) tends to zero. However \(\lim\limits_{x \to 0} f(x)\) doesn’t exist. Continue reading Counterexamples on function limits (part 1) →
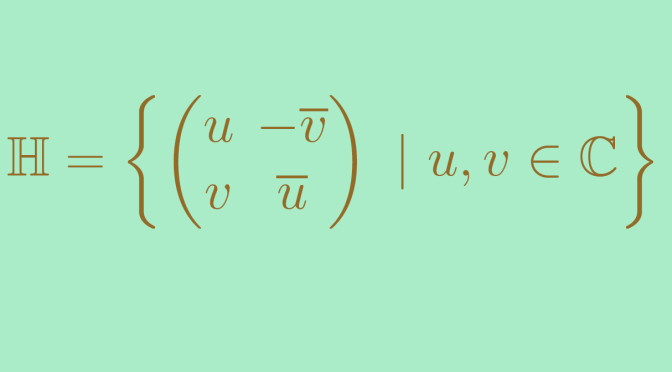
We give here an example of a division ring which is not commutative. According to Wedderburn theorem every finite division ring is commutative. So we must turn to infinite division rings to find a non-commutative one, i.e. a skew field.
Let’s introduce the skew field of the Hamilton’s quaternions \[\mathbb H = \left\{\begin{pmatrix}
u & -\overline{v} \\
v & \overline{u}
\end{pmatrix} \ | \ u,v \in \mathbb C\right\}\] Continue reading The skew field of Hamilton’s quaternions →
Mathematical exceptions to the rules or intuition