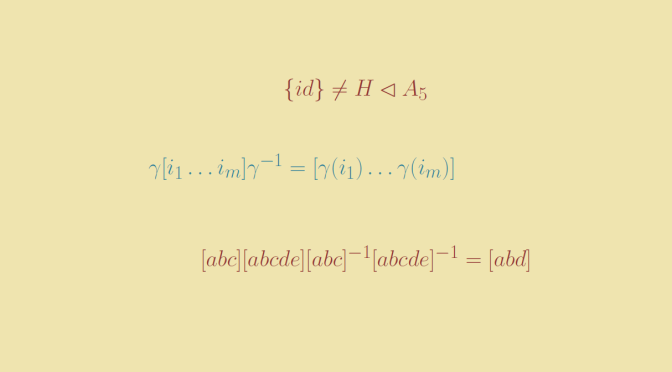Consider a finite group \(G\) whose order (number of elements) is a prime number. It is well known that \(G\) is cyclic and simple. Which means that \(G\) has no non trivial normal subgroup.

Is the converse true, i.e. are the cyclic groups with prime orders the only simple groups? The answer is negative. We prove here that for \(n \ge 5\) the alternating group \(A_n\) is simple. In particular \(A_5\) whose order is equal to \(60\) is simple.

Short recall about the alternating group \(A_n\)

The symmetric group \(S_n\) on the finite set \(\{1,\dots,n\}\) is the group whose elements are all the permutation operations that can be performed on \(\{1,\dots,n\}\). It has \(n!\) elements. The alternating group \(A_n\) is the group of even permutations of \(\{1,\dots,n\}\).

For \(n >1\), the group \(A_n\) is the commutator subgroup of the symmetric group \(S_n\) with index \(2\) and has therefore \(\frac{n!}{2}\) elements.

The symmetric group \(S_n\) is generated by the transpositions, i.e. the permutations that exchange two elements and keep all others fixed. The alternating group \(A_n\) is generated by the set of permutations which are the product of two transpositions.

\(A_n\) is generated by the \(3\)-cycles

As \(A_n\) is generated by the products of two transpositions, it is sufficient to prove that a product of two transpositions is a \(3\)-cycle. Consider the product of two transpositions \([ij][rs]\). If they have two elements in common, it means that \([ij]=[rs]\) and then \([ij][rs]\) is the identity. If they have only one element in common, let say \(j=r\), then \([ij][js] = [ijs]\). If they have no element in common then \[[ij][rs] = [ijr][jrs]\] which is a product of two \(3\) cycles. Finally \([ij][rs]\) is the identity, a \(3\)-cycle or a product of two \(3\)-cycles, so we are done.

If \(n \ge 5\), all \(3\)-cycles are conjugate in \(A_n\)

First let’s recall that if \(\gamma\) is a permutation and \([i_1 \dots i_m]\) is a cycle we have \[\gamma [i_1 \dots i_m] \gamma^{-1} = [\gamma(i_1) \dots \gamma(i_m)]\] Now given two \(3\)-cycles \([ijk]\) and \([i^\prime j^\prime k^\prime]\) there is a permutation \(\gamma\) such that \(\gamma(i)=i^\prime\), \(\gamma(j)=j^\prime\) and \(\gamma(k)=k^\prime\). If \(\gamma\) is even, we are done. If not, we can find \(r,s \notin \{i,j,k\}\) as we supposed \(n \ge 5\). Then \(\gamma_1=\gamma [rs]\) is even and \([rs]\) commutes with \([ijk]\). Hence \[\gamma_1 [ijk] \gamma_1^{-1}=\gamma [rs] [ijk] [rs] \gamma^{-1} = \gamma [ijk] \gamma^{-1} = [i^\prime j^\prime k^\prime]\] proving that all \(3\)-cycles are conjugate in \(A_n\).

If \(n \ge 5\), then the alternating group \(A_n\) is simple

Let \(H\) be a normal subgroup of \(A_n\) different from \(\{id\}\). We prove that \(H\) contains some \(3\)-cycle. According to previous paragraphs this is sufficient to conclude that \(H=A_n\).

Let \(\tau \in H\), \(\tau \neq id\). We can chose \(i\) with \(\tau(i) =j \neq i\) and \(k \notin \{i,j,\tau(j)\}\) as \(n \ge 5\). Now for any \(\sigma \in A_n\), the commutator \(\rho=\sigma \tau \sigma^{-1} \tau^{-1} = (\sigma \tau \sigma^{-1}) \tau^{-1}\) is the product of a conjugate of \(\tau\), which belongs to \(H\) as \(H\) is supposed to be normal, and an element of \(H\). So \(\rho\) belongs to \(H\).

Now take \(\sigma=[ikj]\). We have \[\rho = \sigma (\tau \sigma^{-1} \tau^{-1})=[ijk] (\tau [ijk] \tau^{-1})=[ijk][j \tau(j) \tau(k)]\] Hence \(\rho\) moves only the elements \(\{i,j,k, \tau(k),\tau(j)\}\), i.e. at most five elements.

Also \(\rho\) is an even permutation, which is either the identity, a \(3\)-cycle, a \(5\)-cycle or a product of two transpositions. If \(\rho\) was the identity, we would have \([ijk]=[\tau(k) j \tau (j)]\) which implies \(k=\tau(j)\) in contradiction with our hypothesis \(k \notin \{i,j,\tau(j)\}\). If \(\rho\) is a \(3\)-cycle we are done according to previous paragraphs. If \(\rho=[abcde]\) is a \(5\)-cycle then \[[abc]\rho[abc]^{-1} \rho^{-1}=[abd]\] is a \(3\)-cycle and \(H\) contains a \(3\)-cycle. Finally if \(\rho=[ab][cd]\) \[[abe]\rho[abe]^{-1} \rho^{-1}=[abd]\] is also a \(3\)-cycle contained in \(H\).

Finally \(H=A_n\) is the only possibility and we proved that \(A_n\) is simple.

One can prove that \(A_5\) is the smallest (the one having the lowest order) simple group and that it is the only simple group of order \(60\).