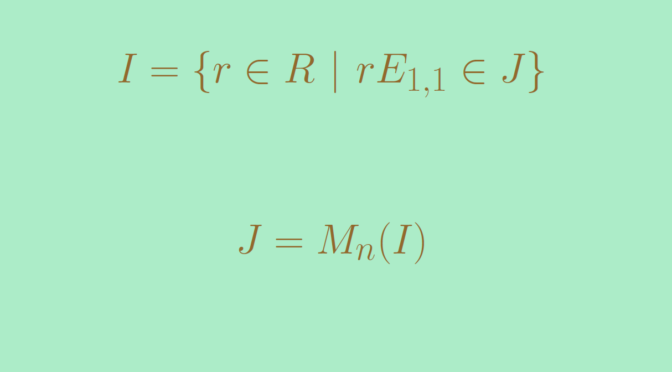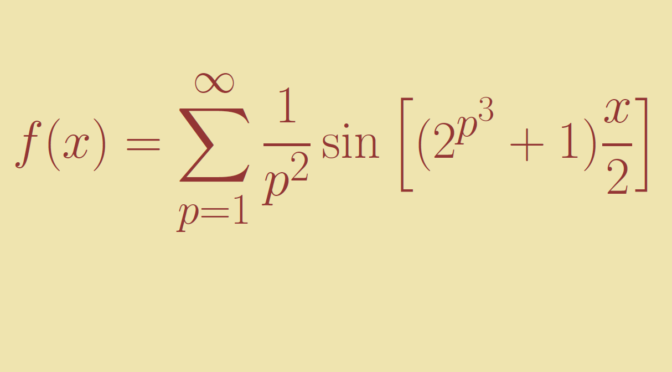Monthly Archives: May 2016

Algebra

A simple ring which is not a division ring

Leave a comment

Let’s recall that a simple ring is a non-zero ring that has no two-sided ideal besides the zero ideal and itself. A division ring is a simple ring. Is the converse true? The answer is negative and we provide here a counterexample of a simple ring which is not a division ring.

We prove that for \(n \ge 1\) the matrix ring \(M_n(F)\) of \(n \times n\) matrices over a field \(F\) is simple. \(M_n(F)\) is obviously not a division ring as the matrix with \(1\) at position \((1,1)\) and \(0\) elsewhere is not invertible.

Let’s prove first following lemma. Continue reading A simple ring which is not a division ring →

Set Theory

Small open sets containing the rationals

Leave a comment

The set \(\mathbb Q\) of the rational number is countable infinite and dense in \(\mathbb R\). You can have a look here on a way to build a bijective map between \(\mathbb N\) and \(\mathbb Q\).

Now given \(\epsilon > 0\), can one find an open set \(O_\epsilon\) of measure less than \(\epsilon\) with \(\mathbb Q \subseteq O_\epsilon\)?

The answer is positive. Let’s denote \[
O_\epsilon = \bigcup_{n \in \mathbb N} (r_n – \frac{\epsilon}{2^{n+1}},r_n + \frac{\epsilon}{2^{n+1}})\] where \((r_n)_{n \in \mathbb N}\) is an enumeration of the rationals. Obviously \(\mathbb Q \subseteq O_\epsilon\). Using countable subadditivity of Lebesgue measure \(\mu\), we get:
\begin{align*}
\mu(O_\epsilon) &\le \sum_{n \in \mathbb N} \mu((r_n – \frac{\epsilon}{2^{n+1}},r_n + \frac{\epsilon}{2^{n+1}}))\\
&= \sum_{n \in \mathbb N} \frac{2 \epsilon}{2^{n+1}} = \sum_{n \in \mathbb N} \frac{\epsilon}{2^n} = \epsilon
\end{align*}

Therefore we’re done. Some additional comments:

  • While Lebesgue measure of the reals is infinite and the rationals are dense in the reals, we can include the rationals in an open set of measure as small as desired!
  • The open segments \((r_n – \frac{\epsilon}{2^{n+1}},r_n + \frac{\epsilon}{2^{n+1}})\) are overlapping. Hence \(\mu(O_\epsilon)\) is strictly less than \(\epsilon\).
Analysis

A continuous function with divergent Fourier series

1 Comment

It is known that for a piecewise continuously differentiable function \(f\), the Fourier series of \(f\) converges at all \(x \in \mathbb R\) to \(\frac{f(x^-)+f(x^+)}{2}\).

We describe Fejér example of a continuous function with divergent Fourier series. Fejér example is the even, \((2 \pi)\)-periodic function \(f\) defined on \([0,\pi]\) by: \[
f(x) = \sum_{p=1}^\infty \frac{1}{p^2} \sin \left[ (2^{p^3} + 1) \frac{x}{2} \right]\]
According to Weierstrass M-test, \(f\) is continuous. We denote \(f\) Fourier series by \[
\frac{1}{2} a_0 + (a_1 \cos x + b_1 \sin x) + \dots + (a_n \cos nx + b_n \sin nx) + \dots.\]

As \(f\) is even, the \(b_n\) are all vanishing. If we denote for all \(m \in \mathbb N\):\[
\lambda_{n,m}=\int_0^{\pi} \sin \left[ (2m + 1) \frac{t}{2} \right] \cos nt \ dt \text{ and } \sigma_{n,m} = \sum_{k=0}^n \lambda_{k,m},\]
we have:\[
\begin{aligned}
a_n &=\frac{1}{\pi} \int_{-\pi}^{\pi} f(t) \cos nt \ dt= \frac{2}{\pi} \int_0^{\pi} f(t) \cos nt \ dt\\
&= \frac{2}{\pi} \int_0^{\pi} \left(\sum_{p=1}^\infty \frac{1}{p^2} \sin \left[ (2^{p^3} + 1) \frac{x}{2} \right]\right) \cos nt \ dt\\
&=\frac{2}{\pi} \sum_{p=1}^\infty \frac{1}{p^2} \int_0^{\pi} \sin \left[ (2^{p^3} + 1) \frac{x}{2} \right] \cos nt \ dt\\
&=\frac{2}{\pi} \sum_{p=1}^\infty \frac{1}{p^2} \lambda_{n,2^{p^3-1}}
\end{aligned}\] One can switch the \(\int\) and \(\sum\) signs as the series is normally convergent.

We now introduce for all \(n \in \mathbb N\):\[
S_n = \frac{\pi}{2} \sum_{k=0}^n a_k = \sum_{p=1}^\infty \sum_{k=0}^n \frac{1}{p^2} \lambda_{k,2^{p^3-1}}
=\sum_{p=1}^\infty \frac{1}{p^2} \sigma_{n,2^{p^3-1}}\]

We will prove below that for all \(n,m \in \mathbb N\) we have \(\sigma_{m,m} \ge \frac{1}{2} \ln m\) and \(\sigma_{n,m} \ge 0\). Assuming those inequalities for now, we get:\[
S_{2^{p^3-1}} \ge \frac{1}{p^2} \sigma_{2^{p^3-1},2^{p^3-1}} \ge \frac{1}{2p^2} \ln(2^{p^3-1}) = \frac{p^3-1}{2p^2} \ln 2\]
As the right hand side diverges to \(\infty\), we can conclude that \((S_n)\) diverges and consequently that the Fourier series of \(f\) diverges at \(0\). Continue reading A continuous function with divergent Fourier series →

Analysis

Radius of convergence of power series

Leave a comment

We look here at the radius of convergence of the sum and product of power series.

Let’s recall that for a power series \(\displaystyle \sum_{n=0}^\infty a_n x^n\) where \(0\) is not the only convergence point, the radius of convergence is the unique real \(0 < R \le \infty\) such that the series converges whenever \(\vert x \vert < R\) and diverges whenever \(\vert x \vert > R\).

Given two power series with radii of convergence \(R_1\) and \(R_2\), i.e.
\begin{align*}
\displaystyle f_1(x) = \sum_{n=0}^\infty a_n x^n, \ \vert x \vert < R_1 \\ \displaystyle f_2(x) = \sum_{n=0}^\infty b_n x^n, \ \vert x \vert < R_2 \end{align*} The sum of the power series \begin{align*} \displaystyle f_1(x) + f_2(x) &= \sum_{n=0}^\infty a_n x^n + \sum_{n=0}^\infty b_n x^n \\ &=\sum_{n=0}^\infty (a_n + b_n) x^n \end{align*} and its Cauchy product:
\begin{align*}
\displaystyle f_1(x) \cdot f_2(x) &= \left(\sum_{n=0}^\infty a_n x^n\right) \cdot \left(\sum_{n=0}^\infty b_n x^n \right) \\
&=\sum_{n=0}^\infty \left( \sum_{l=0}^n a_l b_{n-l}\right) x^n
\end{align*}
both have radii of convergence greater than or equal to \(\min \{R_1,R_2\}\).

The radii can indeed be greater than \(\min \{R_1,R_2\}\). Let’s give examples.
Continue reading Radius of convergence of power series →

Set Theory

A partially ordered set having multiple minimal elements

Leave a comment

Let’s consider a partially ordered set (or poset) \(E\).

If \(E\) is totally ordered, \(E\) has at most one minimal element. If \(E\) is not totally ordered, \(E\) can have multiple minimal elements. We provide an example for the set \(E=\{n \in \mathbb N \ | \ n \ge 2\}\). For two natural numbers \(n\) and \(m\), we write \(n|m\) if \(n\) divides \(m\). One easily sees that this yields a partial order.

The minimal elements of \(E\) are the elements not having divisors, this is the case for all prime numbers \(p \in E\).

\(E\) has an infinite number of minimal elements which are the prime numbers.