I follow on here from the initial article on cardinality. In that article, we have seen that \(\mathbb N\) contains an infinite countable subset whose complement is also infinite. Namely the subsets of even and odd integers.

Let’s now consider the set \(\mathbb N \times \mathbb N\). \(\mathbb N \times \mathbb N\) contains a countable infinite number of copies of \(\mathbb N\), as for all \(i \in \mathbb N\), \(\{i\} \times \mathbb N \subset \mathbb N \times \mathbb N\). Surprisingly, it is however possible to define a bijection between \(\mathbb N \times \mathbb N\) and \(\mathbb N\).

\(\mathbb N \times \mathbb N\) is equinumerous to \(\mathbb N\)

Consider the map \[\begin{array}{l|rcl}
\varphi : & \mathbb N \times \mathbb N & \longrightarrow & \mathbb N\\
& (n,m) & \longmapsto & 2^{n-1} (2m-1) \end{array}\] \(\varphi\) is one-to-one. Suppose that \(2^{n_1-1} (2m_1-1) = 2^{n_2-1} (2m_2-1)\). If \(n_1=1\), we must also have \(n_2=1\) as \(2 m_1 – 1\) is odd. That implies \((n_1,m_1)=(n_2,m_2)\). Let’s now suppose \(n_1 >1\). According to Euclid’s lemma, \(2^{n_1-1}\) divides \(2^{n_2-1}\) as \(2^{n_1-1}\) is even and \(2m_2 – 1\) odd. By symmetry \(2^{n_2-1}\) also divides \(2^{n_1-1}\). Finally, \(2^{n_1 – 1} = 2^{n_2 – 1}\), \(n_1 = n_2\) and consequently \(m_1 = m_2\).

\(\varphi\) is also onto. \(1\) is the image of \((1,1)\) under \(\varphi\). Let’s consider \(r > 1\) integer. According to the unique factorization theorem, \[r=p_1^{r_1} p_2^{r_2} \cdots p_s^{r_s}\] where \(p_1 < \dots < p_s\) is an increasing sequence of primes and \(r_1, \dots, r_s\) positive integers. If \(p_1 = 2\), we get \(r = 2^{(r_1 + 1)-1}(2 \cdot 1 - 1)\) or \(r = 2^{(r_1 + 1)-1}(2 m - 1)\) with \(2m - 1 = p_2^{r_2} \cdots p_s^{r_s}\) depending on whether \(s =1\) or \(s >1\). And if \(p_1 > 2\) we can write \(r = 2^{1 – 1} (2m-1)\) with \(2m-1 = p_1^{r_1} p_2^{r_2} \cdots p_s^{r_s}\) as \(p_1^{r_1} p_2^{r_2} \cdots p_s^{r_s}\) is odd. We have proven that any \(r \in \mathbb N\) has a pre-image under \(\varphi\).

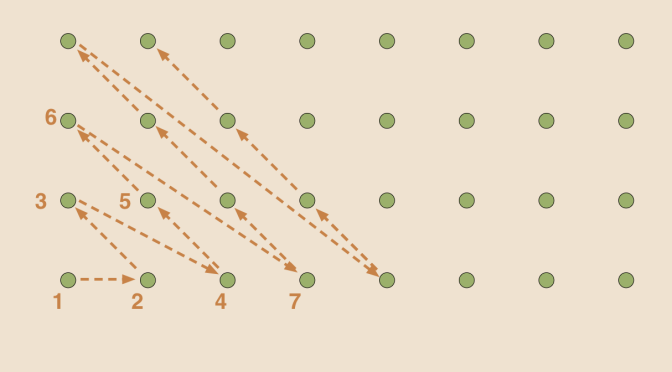
It is possible to define a bijection between \(\mathbb N\) and \(\mathbb N \times \mathbb N\) in a more intuitive way by “counting” the elements of \(\mathbb N \times \mathbb N\) along diagonals as suggested in the image of the article.

To follow on, it’s time to introduce the Schröder–Bernstein theorem which states that for two sets \(E, F\), if there exist a one-to-one map from \(E\) to \(F\) and a one-to-one map from \(F\) to \(E\), there exists a bijection from \(E\) to \(F\).

Based on Schröder–Bernstein theorem, we can move to next paragraph.

\(\mathbb Q\) is equinumerous to \(\mathbb N\)

On one hand, the map
\[\begin{array}{l|rcl}
\varphi_1 : & \mathbb N & \longrightarrow & \mathbb Q\\
& n & \longmapsto & n \end{array}\] is obviously one-to-one.

On the other hand the map \[\begin{array}{l|rcll}
\varphi_2 : & \mathbb Q & \longrightarrow & \mathbb N\\
& 0 & \longmapsto & 0 &\\
& \frac{p}{q} & \longmapsto & 2^p(2q-1) & \mathrm{gcd}(p,q)=1, p >0\\
& \frac{p}{q} & \longmapsto & 2^{-p}(2q-1)+1 & \mathrm{gcd}(p,q)=1, p <0 \end{array}\] is also one-to-one. We can therefore conclude according to Schröder–Bernstein theorem that \(\mathbb Q\) is equinumerous to \(\mathbb N\). This can seem surprising as \(\mathbb Q\) is also dense in \(\mathbb R\), which means that for any \(x < y\) in \(\mathbb R\), one can find \(q \in \mathbb Q\) with \(x < q < y\). While this is clearly not true for \(\mathbb N\).