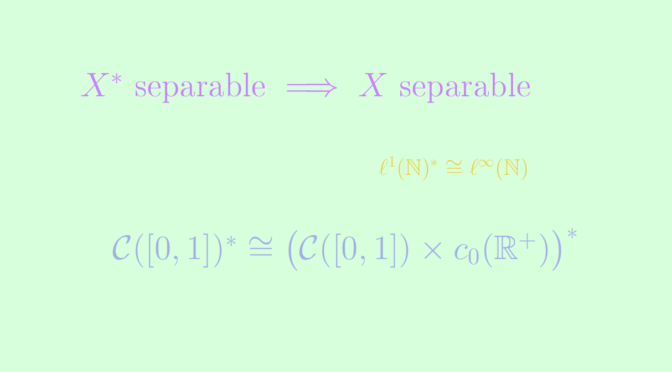separability-dual-image
Topology

Separability of a vector space and its dual

Leave a comment

Recall that a topological space is considered separable when it contains a countable dense set. The following theorem establishes a significant connection between separability and dual spaces:

Theorem: If the dual \(X^*\) of a normed vector space \(X\) is separable, then so is the space \(X\) itself.

Proof outline: let \({f_n}\) be a countable dense set in \(X^*\) unit sphere \(S_*\). For any \(n \in \mathbb{N}\) one can find \(x_n\) in \(X\) unit ball such that \(f_n(x_n) \ge \frac{1}{2}\). We claim that the countable set \(F = \mathrm{Span}_{\mathbb{Q}}(x_0,x_1,…)\) is dense in \(X\). If not, we would find \(x \in X \setminus \overline{F}\) and according to the Hahn-Banach theorem, there would exist a linear functional \(f \in X^*\) such that \(f_{\overline{F}} = 0\) and \(\Vert f \Vert=1\). But then for all \(n \in \mathbb{N}\), \(\Vert f_n-f \Vert \ge \vert f_n(x_n)-f(x_n)\vert = \vert f_n(x_n) \vert \ge \frac{1}{2}\). A contradiction since \({f_n}\) is supposed to be dense in \(S_*\).

We prove that the converse is not true, i.e., a dual space can be separable, while the space itself may not be.

Introducing some normed vector spaces

Given a closed interval \(K \subset \mathbb{R}\) and a set \(A \subset \mathbb{R}\), we define the \(4\) following spaces. The first three are endowed with the supremum norm and the last with the \(\ell^1\) norm.

  • \(\mathcal{C}(K,\mathbb{R})\), the space of continuous functions from \(K\) to \(\mathbb{R}\), is separable as the polynomial functions with coefficients in \(\mathbb{Q}\) are dense and countable.
  • \(\ell^{\infty}(A, \mathbb{R})\) is the space of real bounded functions defined on \(A\) with countable support.
  • \(c_0(A, \mathbb{R}) \subset \ell^{\infty}(A, \mathbb{R})\) is the subspace of elements of \(\ell^{\infty}(A)\) going to \(0\) at \(\infty\).
  • \(\ell^1(A, \mathbb{R})\) is the space of summable functions on \(A\): \(u \in \mathbb{R}^{A}\) is in \(\ell^1(A, \mathbb{R})\) iff \(\sum \limits_{a \in A} |u_x| < +\infty\).

We find the usual sequence spaces when \(A = \mathbb{N}\). It should be noted that \(c_0(A, \mathbb{R})\) and \(\ell^1(A, \mathbb{R})\) are separable iff \(A\) is countable (otherwise the subset \(\big\{x \mapsto 1_{\{a\}}(x),\ a \in A \big\}\) is uncountable, and discrete), and that \(\ell^{\infty}(A, \mathbb{R})\) is separable iff \(A\) is finite (otherwise the subset \(\{0,1\}^A\) is uncountable, and discrete).

We conclude this introduction by reminding that the dual space of \(c_0(A, \mathbb{R})\) is \(\ell^1(A, \mathbb{R})\), and the dual of \(\ell^1(A, \mathbb{R})\) is \(\ell^{\infty}(A, \mathbb{R})\).

Separable space with non-separable dual

An immediate counterexample to the reciprocal of the above theorem is the space \(\ell^1(\mathbb{N}, \mathbb{R})\). It is separable while its dual \(\ell^{\infty}(\mathbb{N}, \mathbb{R})\) is not.

Separable and non-separable spaces with the same dual

A further counterexample is that a separable and a non-separable space can have isometrically isomorphic dual spaces. This example comes from Bill Johnson’s post on MathOverflow.

Consider \(E := \mathcal{C}([0,1],\mathbb{R})\) endowed with the supremum norm. According to theRiesz_representation_theorem, the dual of \(E\) is the space \(\mathcal{M}([0,1])\) of regular signed bounded countably additive measures on \([0,1]\) endowed with the total variation norm.
Any continuous functional \(L \in E^*\) can be represented as \(L(f) = \displaystyle{\int_0^1} f(t)\mu(dt)\) for some signed measure \(\mu \in \mathcal{M}([0,1])\).

The second of our two spaces is \(F := \mathcal{C}([0,1],\mathbb{R}) \times c_0(\mathbb{R}^+, \mathbb{R})\) endowed with the maximum of the two supremum norms. Starting from now, all product spaces will implicitly be endowed with the sum of norms. The dual space of \(F\) is \(\mathcal{M}([0,1]) \times \ell^1(\mathbb{R}^+,\mathbb{R})\).

We will denote respectively \(\mathcal{M}^c([0,1])\) and \(\mathcal{M}^d([0,1])\) the subspaces of continuous measures (measure of any singleton is zero) and discrete measures (concentrated on a discrete set). Then the application \[\begin{aligned}[t]
\mathcal{M}^c([0,1]) \times \mathcal{M}^d([0,1]) &\longrightarrow \mathcal{M}([0,1]) \\
(\mu_c, \mu_d) &\longmapsto \mu_c + \mu_d
\end{aligned}\] is an isomorphism according to Lebesgue’s decomposition theorem. It is quite straightforward to show that \(||\mu_d + \mu_c||_{TV} = ||\mu_d||_{TV} + ||\mu_c||_{TV}\), so the isomorphism is an isometry. Hence \(F^*\) is isometrically isomorphic to:

  • \(\mathcal{M}^c([0,1]) \times \mathcal{M}^d([0,1]) \times \ell^1(\mathbb{R}^+,\mathbb{R})\),
  • \(\mathcal{M}^c([0,1]) \times \mathcal{M}^d([0,1]) \times \ell^1(]1,2],\mathbb{R})\) as \(]1,2]\) is homeomorph to \(\mathbb{R}^+\),
  • \(\mathcal{M}^c([0,1]) \times \mathcal{M}^d([0,1]) \times \mathcal{M}^d(]1,2])\) thanks to the isometry \(f \in \ell^1(]1,2],\mathbb{R}) \mapsto \sum \limits_{x \in ]1,2]} f(x) \delta_x\),
  • \(\mathcal{M}^c([0,1]) \times \mathcal{M}^d([0,2])\) by concatenating the discrete measures,
  • \(\mathcal{M}^c([0,1]) \times \mathcal{M}^d([0,1])\), as \([0,1]\) is homeomorph to \([0,2]\).

We conclude that the dual of \(F\) is isometrically isomorphic to \(\mathcal{M}([0,1])\), the dual of \(E\). Note finally that \(E\) is separable, while \(F\) is not since it contains \(\{0\} \times c_0(\mathbb{R}^+, \mathbb{R})\) which is not separable.

Leave a Reply