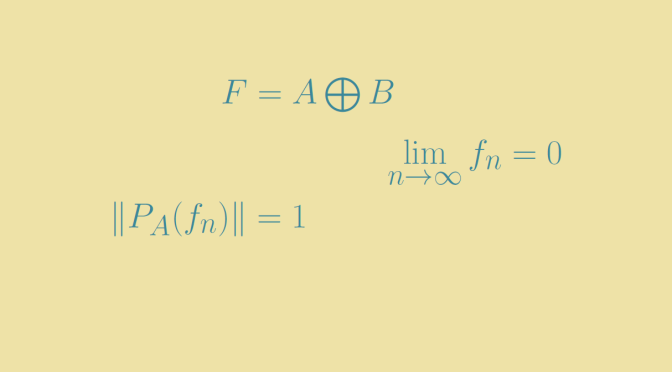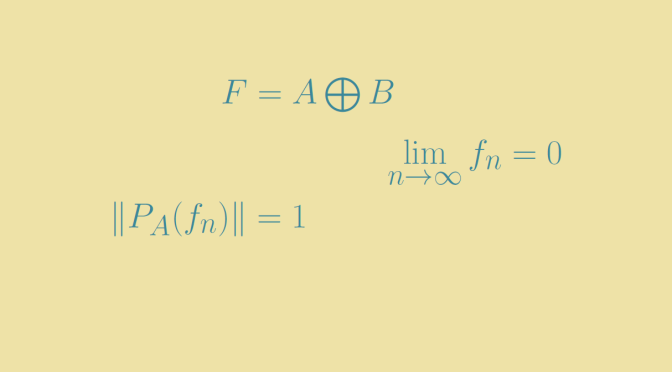
We give here an example of a two complemented subspaces \(A\) and \(B\) that are not topologically complemented.
For this, we consider a vector space of infinite dimension equipped with an inner product. We also suppose that \(E\) is separable. Hence, \(E\) has an orthonormal basis \((e_n)_{n \in \mathbb N}\).
Let \(a_n=e_{2n}\) and \(b_n=e_{2n}+\frac{1}{2n+1} e_{2n+1}\). We denote \(A\) and \(B\) the closures of the linear subspaces generated by the vectors \((a_n)\) and \((b_n)\) respectively. We consider \(F=A+B\) and prove that \(A\) and \(B\) are complemented subspaces in \(F\), but not topologically complemented. Continue reading Two algebraically complemented subspaces that are not topologically complemented →
Let’s start by recalling some background about modules.
Suppose that \(R\) is a ring and \(1_R\) is its multiplicative identity. A left \(R\)-module \(M\) consists of an abelian group \((M, +)\) and an operation \(R \times M \rightarrow M\) such that for all \(r, s \in R\) and \(x, y \in M\), we have:
- \(r \cdot (x+y)= r \cdot x + r \cdot y\) (\( \cdot\) is left-distributive over \(+\))
- \((r +s) \cdot x= r \cdot x + s \cdot x\) (\( \cdot\) is right-distributive over \(+\))
- \((rs) \cdot x= r \cdot (s \cdot x)\)
- \(1_R \cdot x= x \)
\(+\) is the symbol for addition in both \(R\) and \(M\).
If \(K\) is a field, \(M\) is \(K\)-vector space. It is well known that a vector space \(V\) is having a basis, i.e. a subset of linearly independent vectors that spans \(V\).
Unlike for a vector space, a module doesn’t always have a basis. Continue reading A module without a basis →
Mathematical exceptions to the rules or intuition