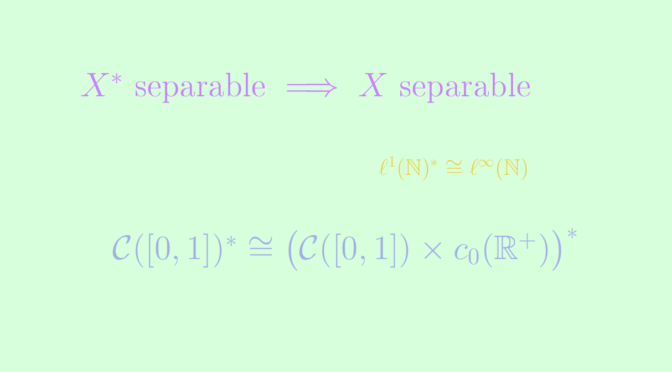Monthly Archives: November 2019

Topology

Separability of a vector space and its dual

Leave a comment

Recall that a topological space is considered separable when it contains a countable dense set. The following theorem establishes a significant connection between separability and dual spaces:

Theorem: If the dual \(X^*\) of a normed vector space \(X\) is separable, then so is the space \(X\) itself.

Proof outline: let \({f_n}\) be a countable dense set in \(X^*\) unit sphere \(S_*\). For any \(n \in \mathbb{N}\) one can find \(x_n\) in \(X\) unit ball such that \(f_n(x_n) \ge \frac{1}{2}\). We claim that the countable set \(F = \mathrm{Span}_{\mathbb{Q}}(x_0,x_1,…)\) is dense in \(X\). If not, we would find \(x \in X \setminus \overline{F}\) and according to the Hahn-Banach theorem, there would exist a linear functional \(f \in X^*\) such that \(f_{\overline{F}} = 0\) and \(\Vert f \Vert=1\). But then for all \(n \in \mathbb{N}\), \(\Vert f_n-f \Vert \ge \vert f_n(x_n)-f(x_n)\vert = \vert f_n(x_n) \vert \ge \frac{1}{2}\). A contradiction since \({f_n}\) is supposed to be dense in \(S_*\).

We prove that the converse is not true, i.e., a dual space can be separable, while the space itself may not be.

Introducing some normed vector spaces

Given a closed interval \(K \subset \mathbb{R}\) and a set \(A \subset \mathbb{R}\), we define the \(4\) following spaces. The first three are endowed with the supremum norm and the last with the \(\ell^1\) norm.

  • \(\mathcal{C}(K,\mathbb{R})\), the space of continuous functions from \(K\) to \(\mathbb{R}\), is separable as the polynomial functions with coefficients in \(\mathbb{Q}\) are dense and countable.
  • \(\ell^{\infty}(A, \mathbb{R})\) is the space of real bounded functions defined on \(A\) with countable support.
  • \(c_0(A, \mathbb{R}) \subset \ell^{\infty}(A, \mathbb{R})\) is the subspace of elements of \(\ell^{\infty}(A)\) going to \(0\) at \(\infty\).
  • \(\ell^1(A, \mathbb{R})\) is the space of summable functions on \(A\): \(u \in \mathbb{R}^{A}\) is in \(\ell^1(A, \mathbb{R})\) iff \(\sum \limits_{a \in A} |u_x| < +\infty\).

We find the usual sequence spaces when \(A = \mathbb{N}\). It should be noted that \(c_0(A, \mathbb{R})\) and \(\ell^1(A, \mathbb{R})\) are separable iff \(A\) is countable (otherwise the subset \(\big\{x \mapsto 1_{\{a\}}(x),\ a \in A \big\}\) is uncountable, and discrete), and that \(\ell^{\infty}(A, \mathbb{R})\) is separable iff \(A\) is finite (otherwise the subset \(\{0,1\}^A\) is uncountable, and discrete).

Continue reading Separability of a vector space and its dual →
Probability

Determinacy of random variables

Leave a comment

The question of the determinacy (or uniqueness) in the moment problem consists in finding whether the moments of a real-valued random variable determine uniquely its distribution. If we assume the random variable to be a.s. bounded, uniqueness is a consequence of Weierstrass approximation theorem.

Given the moments, the distribution need not be unique for unbounded random variables. Carleman’s condition states that for two positive random variables \(X, Y\) with the same finite moments for all orders, if \(\sum\limits_{n \ge 1} \frac{1}{\sqrt[2n]{\mathbb{E}(X^n)}} = +\infty\), then \(X\) and \(Y\) have the same distribution. In this article we describe random variables with different laws but sharing the same moments, on \(\mathbb R_+\) and \(\mathbb N\).

Continuous case on \(\mathbb{R}_+\)

In the article a non-zero function orthogonal to all polynomials, we described a function \(f\) orthogonal to all polynomials in the sense that \[
\forall k \ge 0,\ \displaystyle{\int_0^{+\infty}} x^k f(x)dx = 0 \tag{O}.\]

This function was \(f(u) = \sin\big(u^{\frac{1}{4}}\big)e^{-u^{\frac{1}{4}}}\). This inspires us to define \(U\) and \(V\) with values in \(\mathbb R^+\) by: \[\begin{cases}
f_U(u) &= \frac{1}{24}e^{-\sqrt[4]{u}}\\
f_V(u) &= \frac{1}{24}e^{-\sqrt[4]{u}} \big( 1 + \sin(\sqrt[4]{u})\big)
\end{cases}\]

Both functions are positive. Since \(f\) is orthogonal to the constant map equal to one and \(\displaystyle{\int_0^{+\infty}} f_U = \displaystyle{\int_0^{+\infty}} f_V = 1\), they are indeed densities. One can verify that \(U\) and \(V\) have moments of all orders and \(\mathbb{E}(U^k) = \mathbb{E}(V^k)\) for all \(k \in \mathbb N\) according to orthogonality relation \((\mathrm O)\) above.

Discrete case on \(\mathbb N\)

In this section we define two random variables \(X\) and \(Y\) with values in \(\mathbb N\) having the same moments. Let’s take an integer \(q \ge 2\) and set for all \(n \in \mathbb{N}\): \[
\begin{cases}
\mathbb{P}(X=q^n) &=e^{-q}q^n \cdot \frac{1}{n!} \\
\mathbb{P}(Y=q^n) &= e^{-q}q^n\left(\frac{1}{n!} + \frac{(-1)^n}{(q-1)(q^2-1)\cdot\cdot\cdot (q^n-1)}\right)
\end{cases}\]

Both quantities are positive and for any \(k \ge 0\), \(\mathbb{P}(X=q^n)\) and \(\mathbb{P}(Y=q^n) = O_{n \to \infty}\left(\frac{1}{q^{kn}}\right)\). We are going to prove that for all \(k \ge 1\), \( u_k = \sum \limits_{n=0}^{+\infty} \frac{(-1)^n q^{kn}}{(q-1)(q^2-1)\cdot\cdot\cdot (q^n-1)}\) is equal to \(0\).

Continue reading Determinacy of random variables →