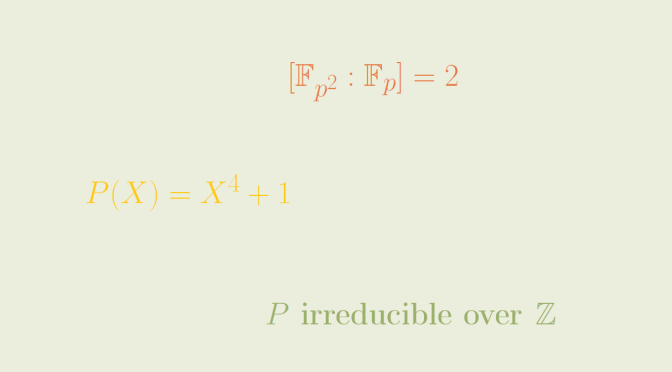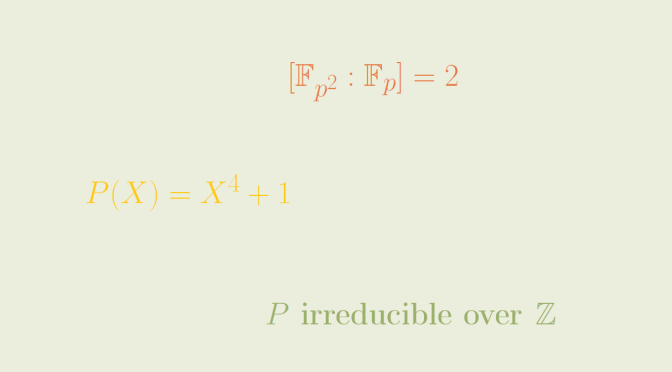
A classical way to prove that an integral polynomial \(Q \in \mathbb{Z}[X]\) is irreducible is to prove that \(Q\) is irreducible over a finite prime field \(\mathbb{F}_p\) where \(p\) is a prime.
This raises the question whether an irreducible integral polynomial is irreducible over at least one finite prime field. The answer is negative and:
\[P(X)=X^4+1\] is a counterexample. Continue reading An irreducible integral polynomial reducible over all finite prime fields
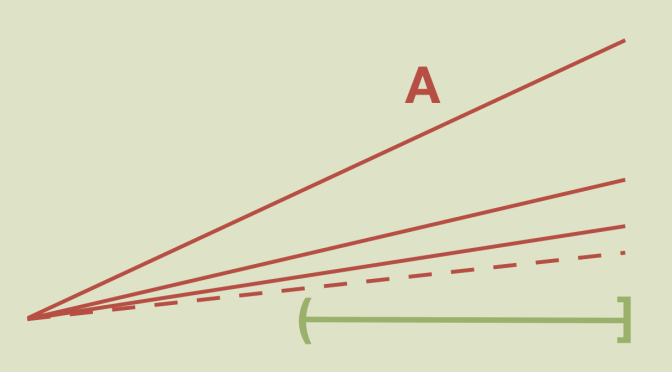
In this article, I will describe a subset of the plane that is a connected space while not locally connected nor path connected.
Let’s consider the plane \(\mathbb{R}^2\) and the two subspaces:
\[A = \bigcup_{n \ge 1} [(0,0),(1,\frac{1}{n})] \text{ and } B = A \cup (\frac{1}{2},1]\] Where a segment noted \(|a,b|\) stands for the plane segment \(|(a,0),(b,0)|\). Continue reading A connected not locally connected space
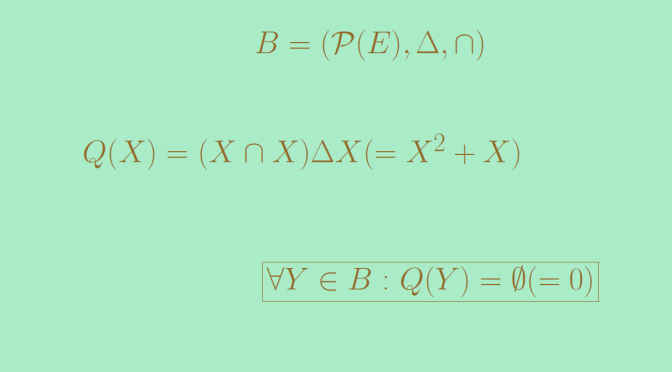
Let’s consider a polynomial of degree \(q \ge 1\) over a field \(K\). It is well known that the sum of the multiplicities of the roots of \(P\) is less or equal to \(q\).
The result remains for polynomials over an integral domain. What is happening for polynomials over a commutative ring? Continue reading On polynomials having more roots than their degree
In that article, I provide basic counterexamples on sequences convergence. I follow on here with some additional and more advanced examples.
This is true and the proof is based on the reverse triangle inequality: \(\bigl| \vert x \vert – \vert y \vert \bigr| \le \vert x – y \vert\). However the converse doesn’t hold. For example, the sequence \(u_n=(-1)^n\) is such that \(\lim \vert u_n \vert = 1\) while \((u_n)\) diverges.
The assertion is wrong. A simple counterexample is \(u_n= \ln(n+1)\). It is well known that \((u_n)\) diverges. However for any \(p \in \mathbb{N}\) we have \(\lim\limits_{n \to +\infty} (u_{n+p} – u_n) =\ln(1+\frac{p}{n+1})=0\).
The converse proposition is true. Assume that \((u_n)\) is a converging sequence with limit \(l\) and \(p \ge 0\) is any integer. We have \(\vert u_{n+p}-u_n \vert = \vert (u_{n+p}-l)-(u_n-l) \vert \le \vert u_{n+p}-l \vert – \vert u_n-l \vert\) and both terms of the right hand side of the inequality are converging to zero. Continue reading Counterexamples on real sequences (part 2)
