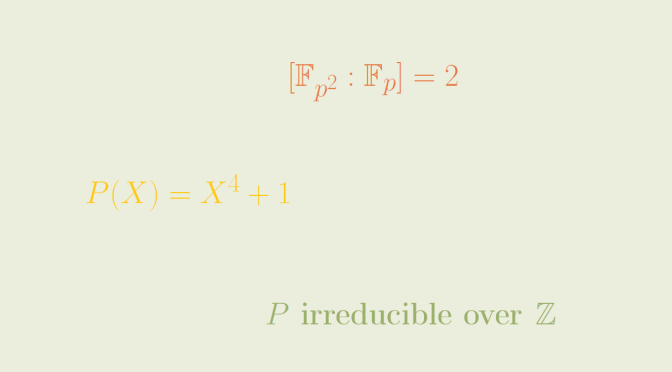A classical way to prove that an integral polynomial \(Q \in \mathbb{Z}[X]\) is irreducible is to prove that \(Q\) is irreducible over a finite prime field \(\mathbb{F}_p\) where \(p\) is a prime.
This raises the question whether an irreducible integral polynomial is irreducible over at least one finite prime field. The answer is negative and:
\[P(X)=X^4+1\] is a counterexample.
\(P\) is irreducible over \(\mathbb{Z}\)
As \(P\) doesn’t have integer roots, if \(P\) was reducible it would be the product of two quadratic polynomials:
\[P(X)=(X^2+aX+b)(X^2+a^\prime X+b^\prime).\] Hence following equations:
\[ \left \{ \begin{array}{lcl}
b b^\prime & = & 1\\
a^\prime b + a b^\prime & = & 0\\
b + b^\prime +a a^\prime & = & 0\\
a + a^\prime & = & 0\\
\end{array} \right .\] Those equations don’t have solutions over \(\mathbb{Z}\) as they imply \(b=b^\prime\), \(\vert b \vert=1\) and \(a=-a^\prime\) and therefore \(2=a^2\) which has no solution over \(\mathbb{Z}\).
\(P\) is reducible over all \(\mathbb{F}_p\) where \(p\) is a prime
\(P\) is reducible over \(\mathbb{F}_2\) as over that field we have:
\[P(X)=X^4+1=(X^2+1)^2\] So let’s now suppose that \(p\) is an odd prime and that \(P\) is irreducible over \(\mathbb{F}_p\). The non-zero elements of the finite field \(\mathbb{F}_{p^2}\) form a multiplicative group \(\mathbb{F}^*_{p^2}\) that is a cyclic group of order \(p^2-1\). As \(p\) is supposed to be odd, it can be written \(p=2r+1\) and \(p^2-1=4r(r+1)\). Therefore \(8\) divides \(p^2-1\) and \(\mathbb{F}_{p^2}\) contains an element \(a\) of order \(8\).
Considering the polynomial:
\[Q(X)=X^8-1=(X^4-1)(X^4+1)\] one can notice that \(a\) is a root of \(Q\) and also of \(P\): \(a\) cannot be a root of \(X^4-1\) as it would be of order \(4\). The multiplicativity formula for degrees gives:
\[2=[\mathbb{F}_{p^2} : \mathbb{F}_p ]=[\mathbb{F}_{p^2} : \mathbb{F}_p(a) ][\mathbb{F}_p(a) : \mathbb{F}_p ]\] leading to a contradiction as \([\mathbb{F}_p(a) : \mathbb{F}_p ] \ge 4\) if \(P\) is supposed to be irreducible over \(\mathbb{F}_p\).