In this article, I consider real valued functions \(f\) defined on \((0,+\infty)\) that converge to zero, i.e.:
\[\lim\limits_{x \to +\infty} f(x) = 0\] If \(f\) is differentiable what can be the behavior of its derivative as \(x\) approaches \(+\infty\)?

Let’s consider a first example:
\[\begin{array}{l|rcl}
f_1 : & (0,+\infty) & \longrightarrow & \mathbb{R} \\
& x & \longmapsto & \frac{1}{x} \end{array}\] \(f_1\) derivative is \(f_1^\prime(x)=-\frac{1}{x^2}\) and we also have \(\lim\limits_{x \to +\infty} f_1^\prime(x) = 0\). Let’s consider more sophisticated cases!

A map converging to \(0\) whose derivative has no limit but is bounded

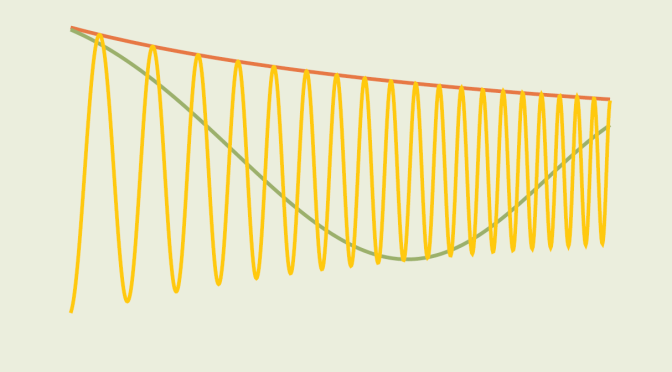
For our second example, consider the map:
\[\begin{array}{l|rcl}
f_2 : & (0,+\infty) & \longrightarrow & \mathbb{R} \\
& x & \longmapsto & \frac{\sin(x^2)}{x} \end{array}\] As the \(\sin\) function is bounded, the limit of \(f_2\) as \(x\) approaches \(+\infty\) is \(0\). What about its derivative \(\displaystyle f_2^\prime(x) = 2 \cos(x^2) – \frac{\sin (x^2)}{x^2}\)? Consider the sequence \(u_n=\sqrt{n \pi}\) for \(n \ge 1\). The value of \(f_2^\prime\) at \(u_n\) is \(2(-1)^n\). As \(\lim\limits_{n \to +\infty} u_n = +\infty\) we can conclude that \(f_2^\prime(x)\) has no limit at \(+\infty\). However for \(x \ge 1\) we have:
\[\vert f_2^\prime(x) \vert \le 2 \vert \cos(x^2) \vert + \left\vert \frac{\sin(x^2)}{x^2} \right\vert \le 3\] so \(f_2^\prime\) is bounded in the neighborhood of \(+\infty\).

A map converging to \(0\) whose derivative has no limit and is unbounded

For our last example, we consider the function:
\[\begin{array}{l|rcl}
f_3 : & (0,+\infty) & \longrightarrow & \mathbb{R} \\
& x & \longmapsto & \frac{\sin(x^3)}{x} \end{array}\] Again the limit of \(f_3\) as \(x\) approaches \(+\infty\) is also \(0\). \(f_3\) derivative is \(\displaystyle f_3^\prime(x) = 3x \cos(x^3) – \frac{\sin (x^3)}{x^2}\).

Consider the sequences:
\[a_n=\sqrt[3]{2 n \pi} \text{ and } b_n=\sqrt[3]{(2n+1) \pi}\] For \(n \ge 1\) we have:
\[f_3^\prime(a_n)=3 a_n \text{ and } f_3^\prime(b_n)=-3 b_n\] The limit of both \((a_n)\) and \((b_n)\) as \(n\) approaches \(+\infty\) is \(\infty\). Therefore \(f_3^\prime\) has no limit and is unbounded in the neighborhood of \(+\infty\).

None of the functions \(f_2\) and \(f_3\) is monotonic. I will come back later on with an example of a decreasing map converging to zero but whose derivative is unbounded in the neighborhood of \(+\infty\).