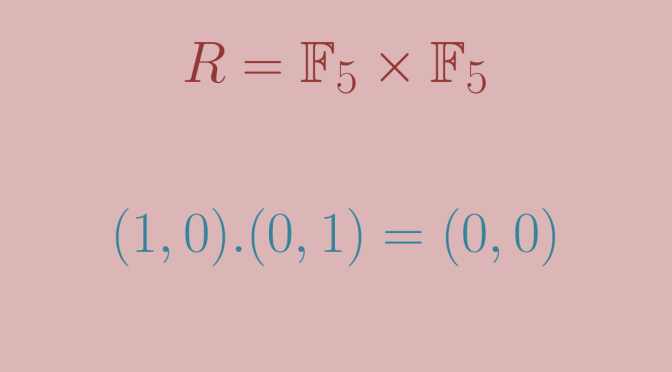Consider a ring \(R\) whose characteristic is a composite number \(p=ab\) with \(a,b\) integers greater than \(1\). Then \(R\) has a zero divisor as we have \[0=p.1=(a.b).1=(a.1).(b.1).\]
What can we say of a ring \(R\) having zero divisors? It is known that the rings \(\mathbb{Z}/p.\mathbb{Z}\) where \(p\) is a prime are fields and therefore do not have zero divisors. Is this a general fact? That is, does a ring whose characteristic is a prime do not have zero divisors?
The answer is negative and we give below a counterexample.
Let’s consider the field \(\mathbb{F}_p = \mathbb{Z}/p.\mathbb{Z}\) where \(p\) is a prime and the product of rings \(R=\mathbb{F}_p \times \mathbb{F}_p\). One can verify following facts:
- \(R\) additive identity is equal to \((0,0)\).
- \(R\) multiplicative identity is equal to \((1,1)\).
- \(R\) is commutative.
- The characteristic of \(R\) is equal to \(p\) as for \(n\) integer, we have \(n.(1,1)=(n.1,n.1)\) which is equal to \((0,0)\) if and only if \(p\) divides \(n\).
However, \(R\) does have zero divisors as following identity holds: \[(1,0).(0,1)=(0,0)\]