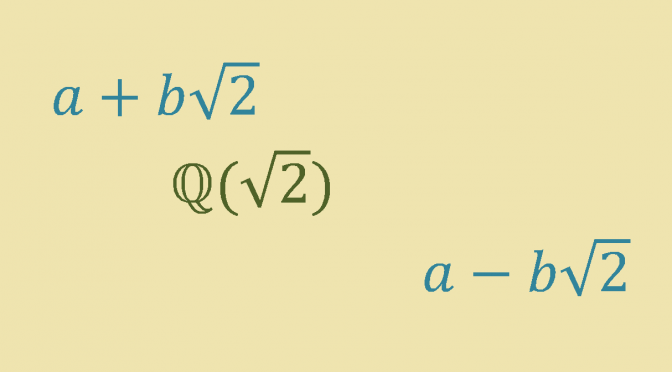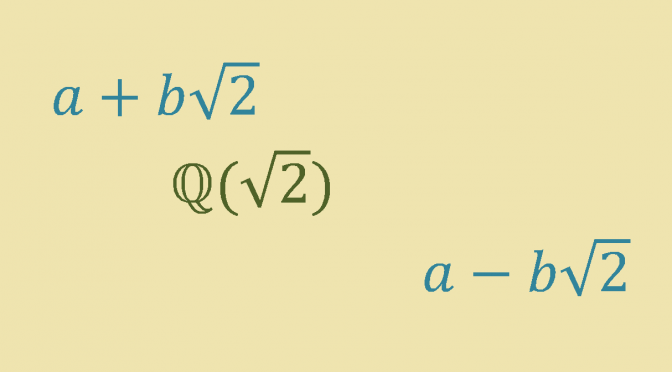
For a short reminder about ordered fields you can have a look to following post. We prove there that \(\mathbb{Q}\) can be ordered in only one way.
That is also the case of \(\mathbb{R}\) as \(\mathbb{R}\) is a real-closed field. And one can prove that the only possible positive cone of a real-closed field is the subset of squares.
However \(\mathbb{Q}(\sqrt{2})\) is a subfield of \(\mathbb{R}\) that can be ordered in two distinct ways. Continue reading A field that can be ordered in two distinct ways →
Introduction to ordered fields
Let \(K\) be a field. An ordering of \(K\) is a subset \(P\) of \(K\) having the following properties:
- ORD 1
- Given \(x \in K\), we have either \(x \in P\), or \(x=0\), or \(-x \in P\), and these three possibilities are mutually exclusive. In other words, \(K\) is the disjoint union of \(P\), \(\{0\}\), and \(-P\).
- ORD 2
- If \(x, y \in P\), then \(x+y\) and \(xy \in P\).
We shall also say that \(K\) is ordered by \(P\), and we call \(P\) the set of positive elements. Continue reading An infinite field that cannot be ordered →

Let \(f_1(x) = |x|\) for \(| x | \le \frac{1}{2}\), and let \(f_1\) be defined for other values of \(x\) by periodic continuation with period \(1\). \(f_1\) graph looks like following picture:
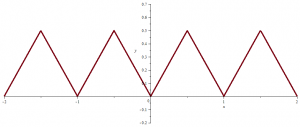
\(f_1\) is continuous everywhere and differentiable on \(\mathbb{R} \setminus \mathbb{Z}\). Continue reading A function that is everywhere continuous and nowhere differentiable →
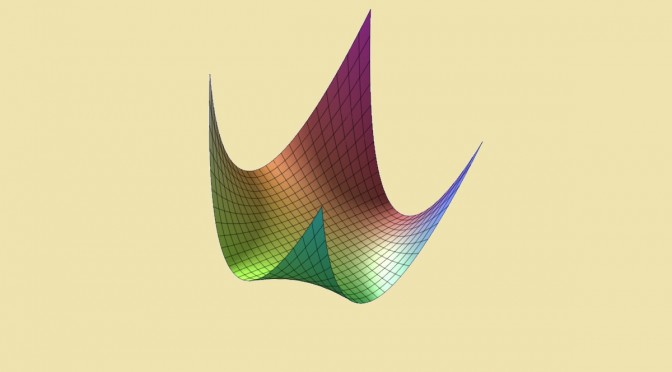
A positive real polynomial function of one variable is always having a minimum.
This is not true for polynomial functions of two variables or more. Continue reading A positive polynomial not reaching its infimum →
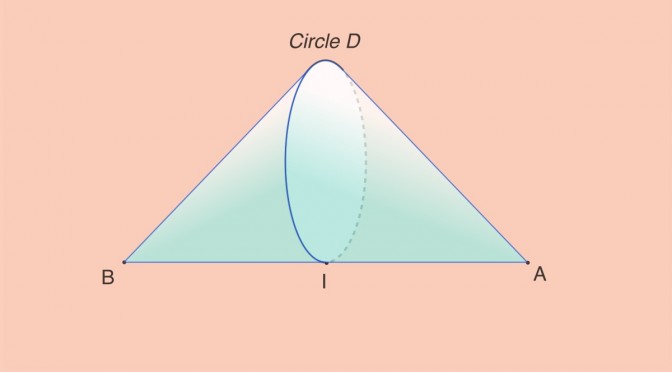
Let’s remind that an extreme point \(c\) of a convex set \(C\) in a real vector space \(E\) is a point in \(C\) which does not lie in any open line segment joining two points of \(C\).
The specific case of dimension \(2\)
Proposition: when \(C\) is closed and its dimension is equal to \(2\), the set \(\hat{C}\) of its extreme points is closed.
Continue reading A compact convex set whose extreme points set is not close →
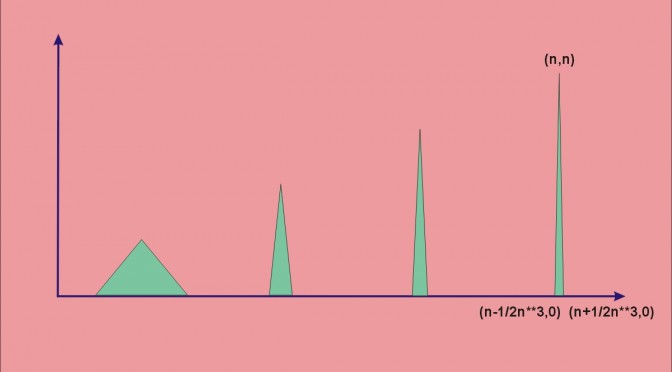
Consider the piecewise linear function \(f\) defined on \([0,+\infty)\) taking following values for all \(n \in \mathbb{N^*}\):
\[
f(x)=
\left\{
\begin{array}{ll}
0 & \mbox{if } x=0\\
0 & \mbox{if } x=n-\frac{1}{2n^3}\\
n & \mbox{if } x=n\\
0 & \mbox{if } x=n+\frac{1}{2n^3}\\
\end{array}
\right.
\]
The graph of \(f\) can be visualized in the featured image of the post. Continue reading An unbounded positive continuous function with finite integral →
Mathematical exceptions to the rules or intuition