Let’s remind that an extreme point \(c\) of a convex set \(C\) in a real vector space \(E\) is a point in \(C\) which does not lie in any open line segment joining two points of \(C\).

The specific case of dimension \(2\)

Proposition: when \(C\) is closed and its dimension is equal to \(2\), the set \(\hat{C}\) of its extreme points is closed.

To prove the proposition, we take a point \(x \notin \hat{C}\) and demonstrate that \(x\) belongs to an open set \(O\) whose intersection with \(\hat{C}\) is empty. That’s clear when \(x \notin C\) as \(C\) is supposed to be closed. If \(x \in C\), there exist \(u,v \in C\) distinct such that \(x\) belongs to the open line segment \((u,v)\).

If a point of the segment \((u,v)\) is in the interior of \(C\), \(x\) itself is in the interior of \(C\) and therefore belongs to an open disk \(O\) included in \(C\). The intersection of \(O\) with \(\hat{C}\) is empty as all points of \(O\) belongs to an open line segment joining two points of \(O \subset C\).

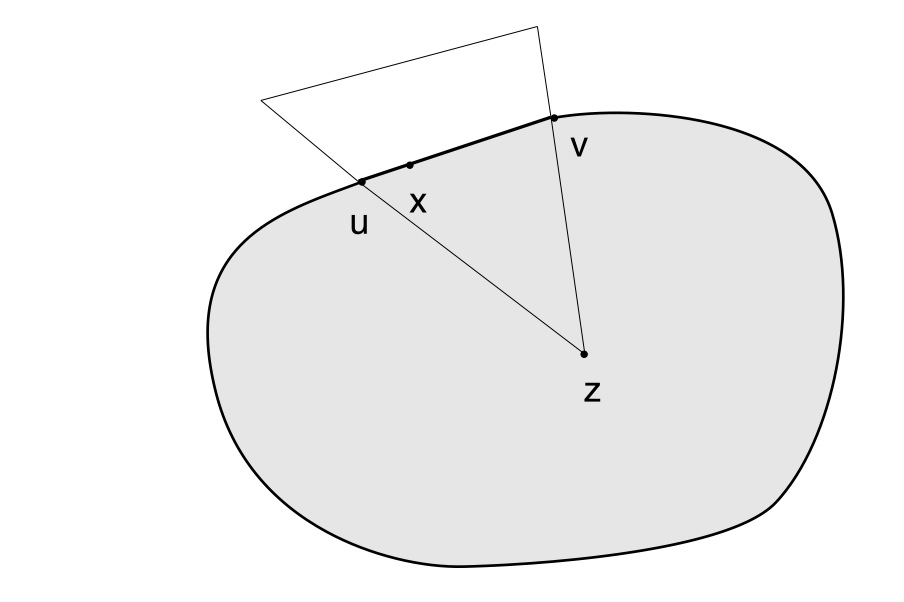Remains the case where the open line segment \((u,v)\) is included in the boundary of \(C\). In that case consider the figure on the right. We can find an open triangle containing \(x\), having a vertex \(z\) in the interior of \(C\) (as \(C\) is of dimension \(2\)) and whose intersection with \(\hat{C}\) is empty. That ends the proof.

The counterexample in dimension \(3\) (or higher)

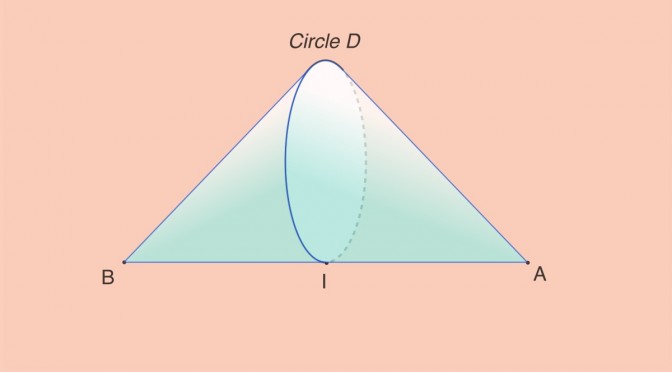
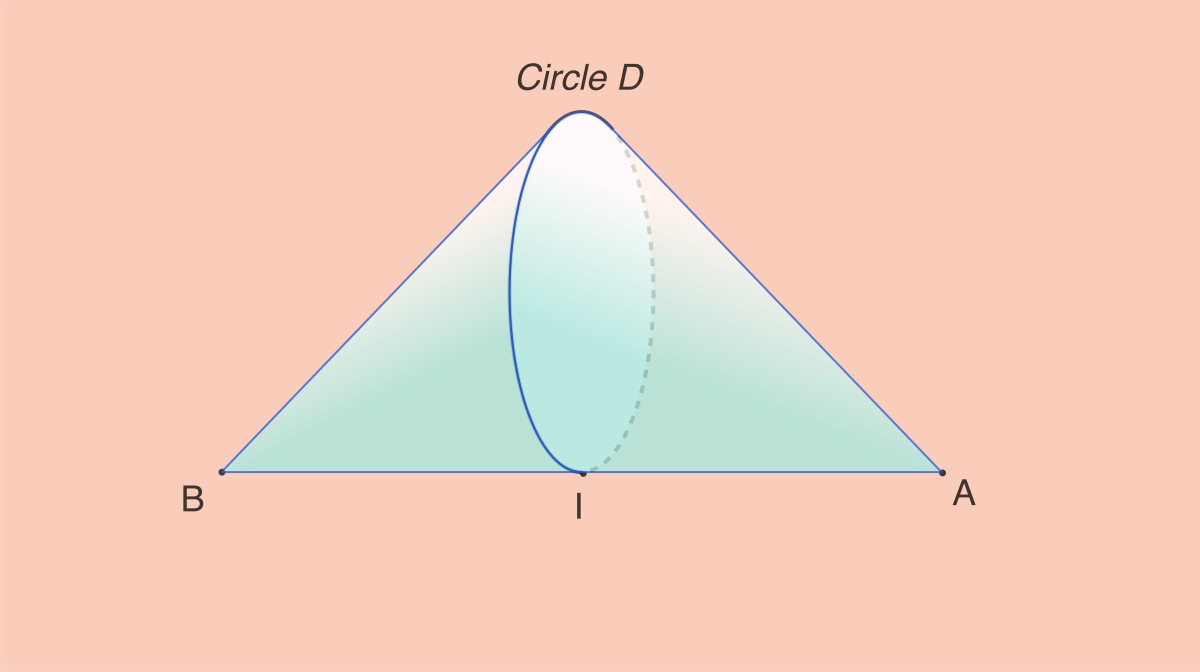In dimension \(3\) a compact convex \(C\) can have a set of extreme points \(\hat{C}\) which is not closed. Take the example of the compact convex consisting of the union of two oblique circular cones like on the left picture. The mid-point \(I\) of the two vertexes \(A\) and \(B\) doesn’t belong to \(\hat{C}\) while all the other points of the circle \(D\) are elements of \(\hat{C}\), therefore \(\hat{C}\) is not close.