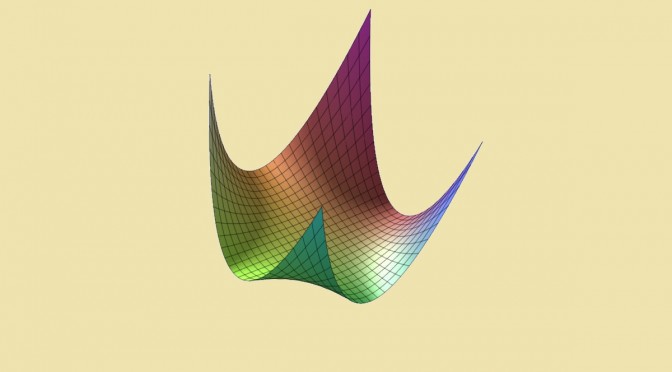
A positive real polynomial function of one variable is always having a minimum.
This is not true for polynomial functions of two variables or more.
Consider the polynomial function:
\[P(x,y)=x^2+(x \cdot y -1)^2\]
\(P\) is obviously positive. Its infimum is \(0\) as \(\lim\limits_{t \to + \infty} P(\frac{1}{t},t) = 0\). However \(P\) never takes \(0\) as a value as this implies the incompatible equations:
\[
\left\{
\begin{array}{l}
x=0\\
x \cdot y =1\\
\end{array}
\right.
\]
See the picture below to have a clue on \(P\) graph.