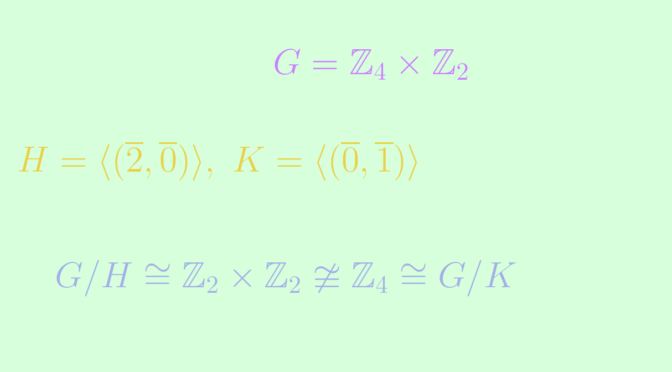Let \(G\) be a group and \(H, K\) two isomorphic subgroups. We provide an example where the quotient groups \(G / H\) and \(G / K\) are not isomorphic.
Let \(G = \mathbb{Z}_4 \times \mathbb{Z}_2\), with \(H = \langle (\overline{2}, \overline{0}) \rangle\) and \(K = \langle (\overline{0}, \overline{1}) \rangle\). We have \[
H \cong K \cong \mathbb{Z}_2.\] The left cosets of \(H\) in \(G\) are \[
G / H=\{(\overline{0}, \overline{0}) + H, (\overline{1}, \overline{0}) + H, (\overline{0}, \overline{1}) + H, (\overline{1}, \overline{1}) + H\},\] a group having \(4\) elements and for all elements \(x \in G/H\), one can verify that \(2x = H\). Hence \(G / H \cong \mathbb{Z}_2 \times \mathbb{Z}_2\). The left cosets of \(K\) in \(G\) are \[
G / K=\{(\overline{0}, \overline{0}) + K, (\overline{1}, \overline{0}) + K, (\overline{2}, \overline{0}) + K, (\overline{3}, \overline{0}) + K\},\] which is a cyclic group of order \(4\) isomorphic to \(\mathbb{Z}_4\). We finally get the desired conclusion \[
G / H \cong \mathbb{Z}_2 \times \mathbb{Z}_2 \ncong \mathbb{Z}_4 \cong G / K.\]