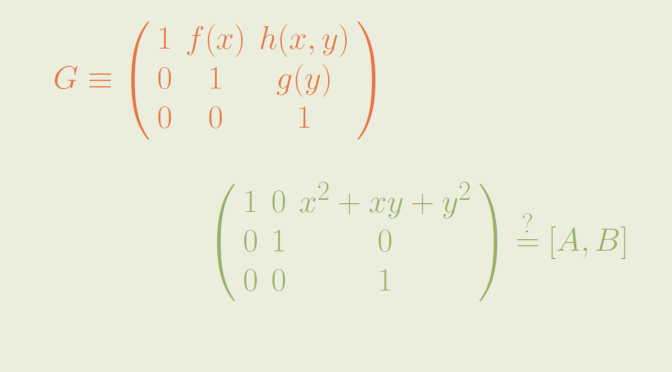I here provide a simple example of a group whose set of commutators is not a subgroup. The counterexample is due to P.J. Cassidy (1979).

Description of the group \(G\)

Let \(k[x,y]\) denote the ring of all polynomials in two variables over a field \(k\), and let \(k[x]\) and \(k[y]\) denote the subrings of all polynomials in \(x\) and in \(y\) respectively. \(G\) is the set of all upper unitriangular matrices of the form
\[A=\left(\begin{array}{ccc}
1 & f(x) & h(x,y) \\
0 & 1 & g(y) \\
0 & 0 & 1 \end{array}\right)\] where \(f(x) \in k[x]\), \(g(y) \in k[y]\), and \(h(x,y) \in k[x,y]\). The matrix \(A\) will also be denoted \((f,g,h)\).
Let’s verify that \(G\) is a group. The products of two elements \((f,g,h)\) and \((f^\prime,g^\prime,h^\prime)\) is
\[\left(\begin{array}{ccc}
1 & f(x) & h(x,y) \\
0 & 1 & g(y) \\
0 & 0 & 1 \end{array}\right)
\left(\begin{array}{ccc}
1 & f^\prime(x) & h^\prime(x,y) \\
0 & 1 & g^\prime(y) \\
0 & 0 & 1 \end{array}\right)\]
\[=\left(\begin{array}{ccc}
1 & f(x)+f^\prime(x) & h(x,y)+h^\prime(x,y)+f(x)g^\prime(y) \\
0 & 1 & g(y)+g^\prime(y) \\
0 & 0 & 1 \end{array}\right)\] which is an element of \(G\). We also have:
\[\left(\begin{array}{ccc}
1 & f(x) & h(x,y) \\
0 & 1 & g(y) \\
0 & 0 & 1 \end{array}\right)^{-1} =
\left(\begin{array}{ccc}
1 & -f(x) & f(x)g(y) – h(x,y) \\
0 & 1 & -g(y) \\
0 & 0 & 1 \end{array}\right)\] proving that the inverse of an element of \(G\) is also an element of \(G\).

The commutator subgroup of \(G\) is the set of elements \((0,0,h)\) where \(h \in k[x,y]\)

Let’s remind that the commutator subgroup of a group is the subgroup generated by all the commutators of the group. For elements \(a\) and \(b\) of a group, the commutator of \(a\) and \(b\) is \([a,b]=a^{-1}b^{-1}ab\). The commutator subgroup of \(G\), also called the derived subgroup is denoted \(G^\prime\). One can verify that the commutator of \((f,g,h), \ (f^\prime,g^\prime,h^\prime) \in G\) is
\[[(f,g,h),(f^\prime,g^\prime,h^\prime)]=
\left(\begin{array}{ccc}
1 & 0 & f(x)g^\prime(y)-f^\prime(x)g(y) \\
0 & 1 & 0 \\
0 & 0 & 1 \end{array}\right)\] which is an element \((0,0,h(x,y))\) with \(h(x,y)=f(x)g^\prime(y)-f^\prime(x)g(y) \in k[x,y]\). Conversely, we have to prove that for \(\displaystyle h(x,y) \in k[x,y]\), \((0,0,h(x,y))\) belongs to \(G^\prime\). When \(h(x,y)=x^ky^l\) is a monomial, we derive from above the equality \((0,0,x^ky^l)=[(x^k,0,0)(0,y^l,0)]\) which proves that \((0,0,x^ky^l)\) is a commutator. The following equality
\[\left(\begin{array}{ccc}
1 & 0 & a \\
0 & 1 & 0 \\
0 & 0 & 1 \end{array}\right)
\left(\begin{array}{ccc}
1 & 0 & b \\
0 & 1 & 0 \\
0 & 0 & 1 \end{array}\right)=
\left(\begin{array}{ccc}
1 & 0 & a+b \\
0 & 1 & 0 \\
0 & 0 & 1 \end{array}\right)\] holds. Hence we get
\[(0,0,h)=\prod_{i,j}[(a_{ij}x^i,0,0),(0,y^j,0)]\] for any \(\displaystyle h(x,y)=\sum_{i,j} a_{ij}x^iy^j \in k[x,y]\). We can finally conclude
\[G^\prime=\{(0,0,h(x,y)) | \ h(x,y) \in k[x,y]\}\]

\((0,0,x^2+xy+y^2)\) is not a commutator

If \((0,0,x^2+xy+y^2)\) is a commutator, then there are polynomials \(f(x),f^\prime(x) \in k[x]\) and \(g(y),g^\prime(y) \in k[y]\) with
\[x^2+xy+y^2=f(x)g^\prime(y)-f^\prime(x)g(y)\] If \(f(x) = \sum b_i x^i\) and \(f^\prime(x) = \sum b_i^\prime x^i\), then there are equations:
\[\left\{\begin{array}{lll}
b_0 g^\prime(y) – b_0^\prime g(y) & = & y^2 \\
b_1 g^\prime(y) – b_1^\prime g(y) & = & y \\
b_2 g^\prime(y) – b_2^\prime g(y) & = & 1 \end{array}\right.\] which cannot be as this implies that the two polynomials \(g(y),g^\prime(y)\) generate the three linearly independent polynomials \(\{1,y,y^2\}\).
Based on this result, we derive that the product of the two commutators \([(x^2,-y,0)(x,1,0)]=(0,0,x^2+xy)\) and \([(0,y^2,0)(0,0,0)]=(0,0,y^2)\) which is equal to \((0,0,x^2+xy+y^2)\) is not a commutator.

Case of finite groups

The group \(G\) is infinite. It is also possible to find a finite group whose set of commutator is not a subgroup. I might come back on this topic later on. The smallest group having this feature is of order \(96\).