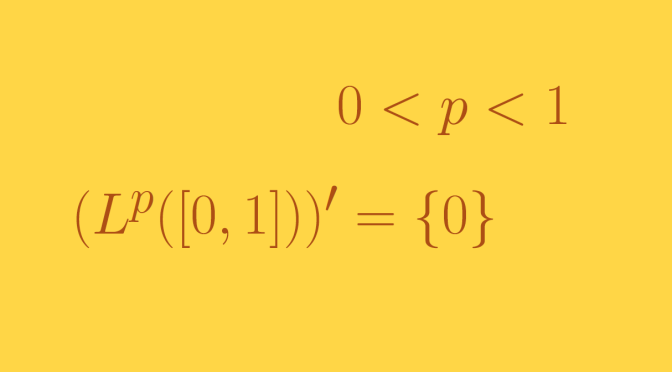We consider here the \(L^p\)- spaces of real functions defined on \([0,1]\) for which the \(p\)-th power of the absolute value is Lebesgue integrable. We focus on the case \(0 < p < 1\). We'll prove that those \(L^p\)-spaces are topological vector spaces on which there exists no continuous non-trivial linear forms (i.e. not vanishing identically).

The elements of \(L^p\) are those Lebesgue measurable functions \(f\) on \([0, 1]\) for which:
\[\Delta(f)=\int_0^1 \vert f(t) \vert^p dt < \infty\] Since \(0 < p < 1\), the inequality \[(a+b)^p \le a^p + b^p\] holds for \(a \ge 0\) and \(b \ge 0\). This gives \[\Delta(f+g) \le \Delta(f) + \Delta(g)\] so that \[d(f,g) = \Delta(f-g)\] is an invariant metric on \(L^p\). This metric induces a topology on the space \(L^p\). Equipped with this topology, \(L^p\) is a topological vector space as the maps \((x,y) \mapsto x+y\) from \(L^p \times L^p\) into \(L^p\) and \((\lambda,x) \mapsto \lambda x\) from \(\mathbb{R} \times L^p\) into \(L^p\) are continuous.

\(L^p\) (\(0 < p < 1\)) contains no convex open sets other than \(\emptyset\) and \(L^p\)

Suppose that \(V\) is a non-empty convex open set in \(L^p\). We can assume that \(0 \in V\) possibly using a translation. As \(V\) is open, one can find \(r > 0\) with \(B_r = \{f \in L^p \text{ : } \Delta(f) < r\} \subset V\). Pick \(f \in L^p\). Since \(p < 1\), there is a positive integer \(n\) such that \(n^{p-1} \Delta(f) < r\). By the continuity of the indefinite integral of \(\vert f \vert^p\), there are points \(0 = x_0 < x_1 < \dots < x_n=1\) such that \[\int_{x_{i-1}}^{x_i} \vert f(t) \vert^p dt = \frac{\Delta(f)}{n} \text{ for } 1 \le i \le n\] For \(1 \le i \le n\) define \(g_i(t)=nf(t)\) for \(x_{i-1} < t \le x_i\), \(g_i(t)=0\) otherwise. We have: \[\Delta(g_i)=\int_{x_{i-1}}^{x_i} \vert nf(t) \vert^p dt=n^{p-1} \Delta(f) < r\] Hence \(g_i \in B_r\) and \(g_i \in V\) as \(B_r \subset V\). Since \(V\) is supposed to be convex and \(f=\frac{1}{n}(g_1+\dots+g_n)\) it follows that \(f \in V\). Therefore \(V = L^p\).

There exists no continuous non-trivial linear form on \(L^p\)

Suppose \(\Lambda: \ L^p \to \mathbb{R}\) is a continuous linear form. The inverse image of the open convex subset \((-1,1) \subset \mathbb{R}\) under \(\Lambda\) is convex as \(\Lambda\) is linear and open as \(\Lambda\) is continuous. According to previous paragraph, if \(\Lambda\) is not vanishing identically, \(\Lambda^{-1}((-1,1)) = L^p\) which is not possible. Therefore \(0\) is the only continuous linear form.