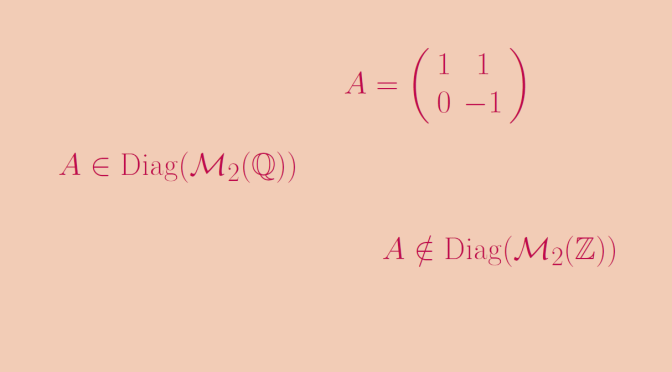Let us recall that a square matrix \(A\) is called diagonalizable if it is similar to a diagonal matrix, i.e. if there exists an invertible matrix \(P\) such that \(P^{-1}AP\) is a diagonal matrix. Continue reading A diagonalizable matrix over Q but not over Z
Monthly Archives: March 2015
A decreasing function converging to zero whose derivative diverges (part2)
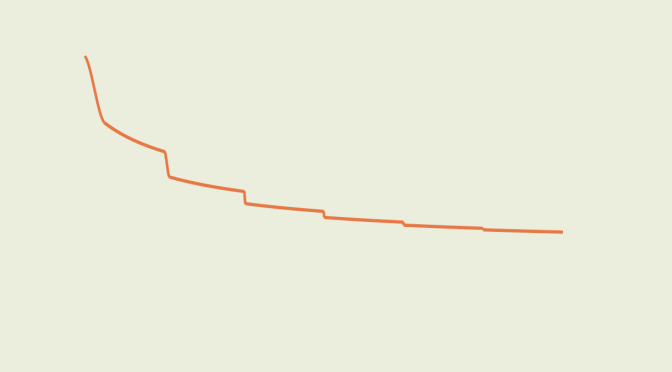
In that article, I gave examples of real valued functions defined on \((0,+\infty)\) that converge to zero and whose derivatives diverge. But those functions were not monotonic. Here I give an example of a decreasing real valued function \(g\) converging to zero at \(+\infty\) and whose derivative is unbounded.
We first consider the polynomial map:
\[P(x)=(1+2x)(1-x)^2=1-3x^2+2x^3\] on the segment \(I=[0,1]\). \(P\) derivative equals \(P^\prime(x)=-6x(1-x)\). Therefore \(P\) is decreasing on \(I\). Moreover we have \(P(0)=1\), \(P(1)=P^\prime(0)=P^\prime(1)=0\) and \(P^\prime(1/2)=-3/2\). Continue reading A decreasing function converging to zero whose derivative diverges (part2)
One matrix having several interesting properties
We consider a vector space \(V\) of dimension \(2\) over a field \(\mathbb{K}\). The matrix:
\[A=\left( \begin{array}{cc}
0 & 1 \\
0 & 0 \end{array} \right)\] has several wonderful properties!
Only zero as eigenvalue, but minimal polynomial of degree \(2\)
Zero is the only eigenvalue. The corresponding characteristic space is \(\mathbb{K} . e_1\) where \((e_1,e_2)\) is the standard basis. The minimal polynomial of \(A\) is \(\mu_A(X)=X^2\). Continue reading One matrix having several interesting properties
A separable space that is not second-countable
In topology, a second-countable space (also called a completely separable space) is a topological space having a countable base.
It is well known that a second-countable space is separable. For the proof consider a second-countable space \(X\) with countable basis \(\mathcal{B}=\{B_n; n \in \mathbb{N}\}\). We can assume without loss of generality that all the \(B_n\) are nonempty, as the empty ones can be discarded. Now, for each \(B_n\), pick any element \(b_n\). Let \(D=\{b_n;n \in \mathbb{N}\}\). \(D\) is countable. We claim that \(D\) is dense in \(X\). To see this let \(U\) be any nonempty open subset of \(X\). \(U\) contains some \(B_p\), hence \(b_p \in U\). So \(D\) intersects \(U\) proving that \(D\) is dense.
What about the converse? Is a separable space second-countable? The answer is negative and I present below a counterexample. Continue reading A separable space that is not second-countable
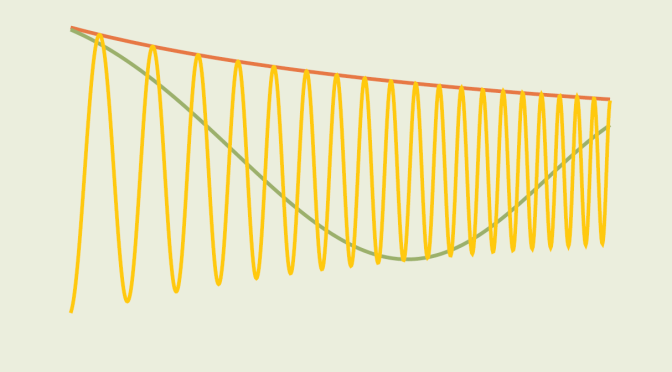
Differentiable functions converging to zero whose derivatives diverge (part1)
In this article, I consider real valued functions \(f\) defined on \((0,+\infty)\) that converge to zero, i.e.:
\[\lim\limits_{x \to +\infty} f(x) = 0\] If \(f\) is differentiable what can be the behavior of its derivative as \(x\) approaches \(+\infty\)?
Let’s consider a first example:
\[\begin{array}{l|rcl}
f_1 : & (0,+\infty) & \longrightarrow & \mathbb{R} \\
& x & \longmapsto & \frac{1}{x} \end{array}\] \(f_1\) derivative is \(f_1^\prime(x)=-\frac{1}{x^2}\) and we also have \(\lim\limits_{x \to +\infty} f_1^\prime(x) = 0\). Let’s consider more sophisticated cases! Continue reading Differentiable functions converging to zero whose derivatives diverge (part1)