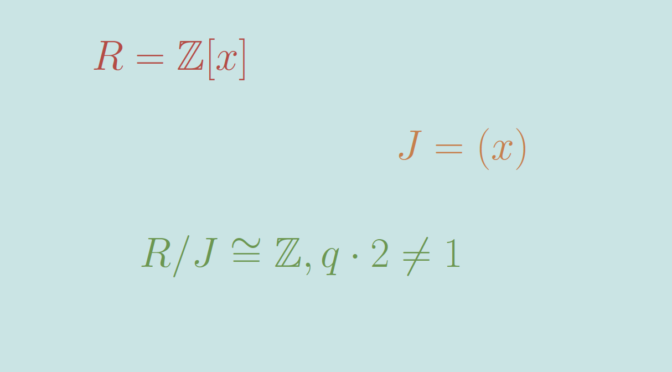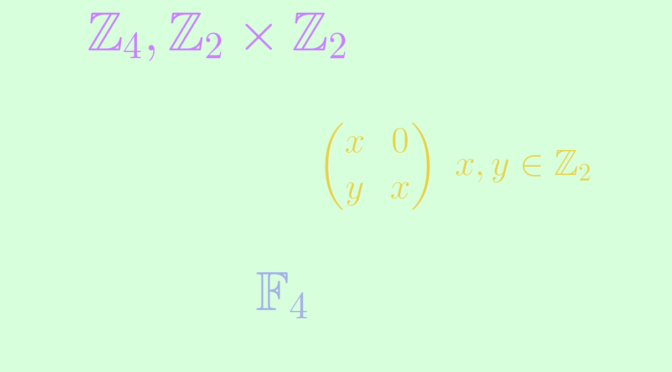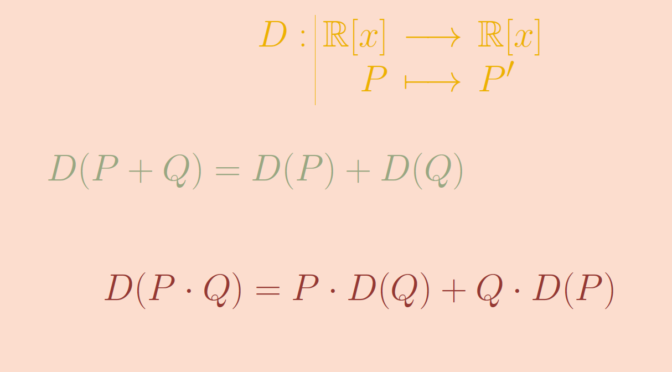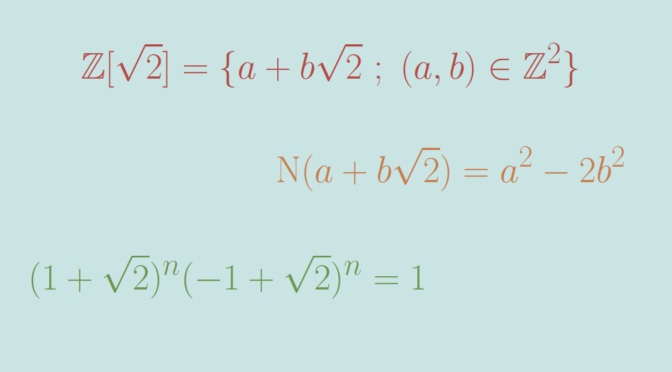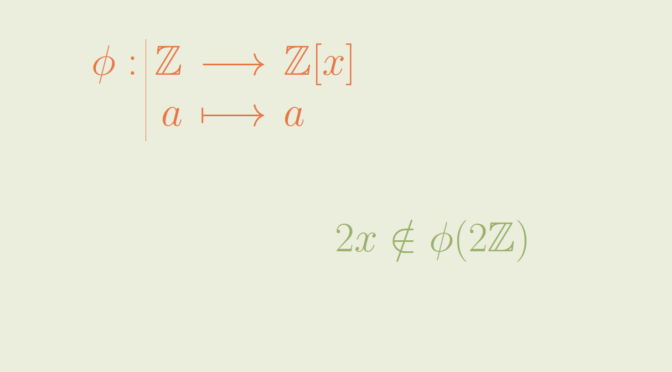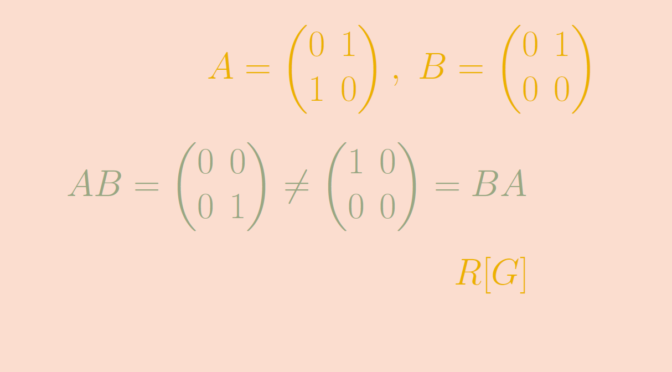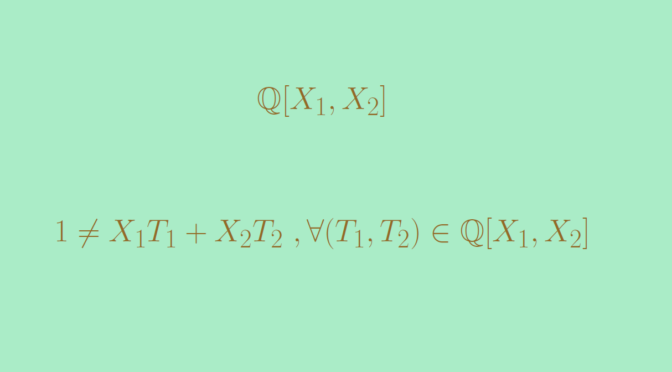Would you like to be the contributor for the 100th ring on the Database of Ring Theory? Go here!
Tag Archives: rings
A prime ideal that is not a maximal ideal
Every maximal ideal is a prime ideal. The converse is true in a principal ideal domain – PID, i.e. every nonzero prime ideal is maximal in a PID, but this is not true in general. Let’s produce a counterexample.
\(R= \mathbb Z[x]\) is a ring. \(R\) is not a PID as can be shown considering the ideal \(I\) generated by the set \(\{2,x\}\). \(I\) cannot be generated by a single element \(p\). If it was, \(p\) would divide \(2\), i.e. \(p=1\) or \(p=2\). We can’t have \(p=1\) as it means \(R = I\) but \(3 \notin I\). We can’t have either \(p=2\) as it implies the contradiction \(x \notin I\). The ideal \(J = (x)\) is a prime ideal as \(R/J \cong \mathbb Z\) is an integral domain. Since \(\mathbb Z\) is not a field, \(J\) is not a maximal ideal.
Four elements rings
A group with four elements is isomorphic to either the cyclic group \(\mathbb Z_4\) or to the Klein four-group \(\mathbb Z_2 \times \mathbb Z_2\). Those groups are commutative. Endowed with the usual additive and multiplicative operations, \(\mathbb Z_4\) and \(\mathbb Z_2 \times \mathbb Z_2\) are commutative rings.
Are all four elements rings also isomorphic to either \(\mathbb Z_4\) or \(\mathbb Z_2 \times \mathbb Z_2\)? The answer is negative. Let’s provide two additional examples of commutative rings with four elements not isomorphic to \(\mathbb Z_4\) or \(\mathbb Z_2 \times \mathbb Z_2\).
The first one is the field \(\mathbb F_4\). \(\mathbb F_4\) is a commutative ring with four elements. It is not isomorphic to \(\mathbb Z_4\) or \(\mathbb Z_2 \times \mathbb Z_2\) as both of those rings have zero divisor. Indeed we have \(2 \cdot 2 = 0\) in \(\mathbb Z_4\) and \((1,0) \cdot (0,1)=(0,0)\) in \(\mathbb Z_2 \times \mathbb Z_2\).
A second one is the ring \(R\) of the matrices \(\begin{pmatrix}
x & 0\\
y & x\end{pmatrix}\) where \(x,y \in \mathbb Z_2\). One can easily verify that \(R\) is a commutative subring of the ring \(M_2(\mathbb Z_2)\). It is not isomorphic to \(\mathbb Z_4\) as its characteristic is \(2\). This is not isomorphic to \(\mathbb Z_2 \times \mathbb Z_2\) either as \(\begin{pmatrix}
0 & 0\\
1 & 0\end{pmatrix}\) is a non-zero matrix solution of the equation \(X^2=0\). \((0,0)\) is the only solution of that equation in \(\mathbb Z_2 \times \mathbb Z_2\).
One can prove that the four rings mentioned above are the only commutative rings with four elements up to isomorphism.
Group homomorphism versus ring homomorphism
A ring homomorphism is a function between two rings which respects the structure. Let’s provide examples of functions between rings which respect the addition or the multiplication but not both.
An additive group homomorphism that is not a ring homomorphism
We consider the ring \(\mathbb R[x]\) of real polynomials and the derivation \[
\begin{array}{l|rcl}
D : & \mathbb R[x] & \longrightarrow & \mathbb R[x] \\
& P & \longmapsto & P^\prime \end{array}\] \(D\) is an additive homomorphism as for all \(P,Q \in \mathbb R[x]\) we have \(D(P+Q) = D(P) + D(Q)\). However, \(D\) does not respect the multiplication as \[
D(x^2) = 2x \neq 1 = D(x) \cdot D(x).\] More generally, \(D\) satisfies the Leibniz rule \[
D(P \cdot Q) = P \cdot D(Q) + Q \cdot D(P).\]
A multiplication group homomorphism that is not a ring homomorphism
The function \[
\begin{array}{l|rcl}
f : & \mathbb R & \longrightarrow & \mathbb R \\
& x & \longmapsto & x^2 \end{array}\] is a multiplicative group homomorphism of the group \((\mathbb R, \cdot)\). However \(f\) does not respect the addition.
A Commutative Ring with Infinitely Many Units
In a ring \(R\) a unit is any element \(u\) that has a multiplicative inverse \(v\), i.e. an element \(v\) such that \[
uv=vu=1,\] where \(1\) is the multiplicative identity.
The only units of the commutative ring \(\mathbb Z\) are \(-1\) and \(1\). For a field \(\mathbb F\) the units of the ring \(\mathrm M_n(\mathbb F)\) of the square matrices of dimension \(n \times n\) is the general linear group \(\mathrm{GL}_n(\mathbb F)\) of the invertible matrices. The group \(\mathrm{GL}_n(\mathbb F)\) is infinite if \(\mathbb F\) is infinite, but the ring \(\mathrm M_n(\mathbb F)\) is not commutative for \(n \ge 2\).
The commutative ring \(\mathbb Z[\sqrt{2}] = \{a + b\sqrt{2} \ ; \ (a,b) \in \mathbb Z^2\}\) is not a field. However it has infinitely many units.
\(a + b\sqrt{2}\) is a unit if and only if \(a^2-2b^2 = \pm 1\)
For \(u = a + b\sqrt{2} \in \mathbb Z[\sqrt{2}]\) we denote \(\mathrm N(u) = a^2- 2b^2 \in \mathbb Z\). For any \(u,v \in \mathbb Z[\sqrt{2}]\) we have \(\mathrm N(uv) = \mathrm N(u) \mathrm N(v)\). Therefore for a unit \(u \in \mathbb Z[\sqrt{2}]\) with \(v\) as multiplicative inverse, we have \(\mathrm N(u) \mathrm N(v) = 1\) and \(\mathrm N(u) =a^2-2b^2 \in \{-1,1\}\).
The elements \((1+\sqrt{2})^n\) for \(n \in \mathbb N\) are unit elements
The proof is simple as for \(n \in \mathbb N\) \[
(1+\sqrt{2})^n (-1 + \sqrt{2})^n = \left((1+\sqrt{2})(-1 + \sqrt{2})\right)^n=1\]
One can prove (by induction on \(b\)) that the elements \((1+\sqrt{2})^n\) are the only units \(u \in \mathbb Z[\sqrt{2}]\) for \(u \gt 1\).
The image of an ideal may not be an ideal
If \(\phi : A \to B\) is a ring homomorphism then the image of a subring \(S \subset A\) is a subring \(\phi(A) \subset B\). Is the image of an ideal under a ring homomorphism also an ideal? The answer is negative. Let’s provide a simple counterexample.
Let’s take \(A=\mathbb Z\) the ring of the integers and for \(B\) the ring of the polynomials with integer coefficients \(\mathbb Z[x]\). The inclusion \(\phi : \mathbb Z \to \mathbb Z[x]\) is a ring homorphism. The subset \(2 \mathbb Z \subset \mathbb Z\) of even integers is an ideal. However \(2 \mathbb Z\) is not an ideal of \(\mathbb Z[x]\) as for example \(2x \notin 2\mathbb Z\).
Non commutative rings
Let’s recall that a set \(R\) equipped with two operations \((R,+,\cdot)\) is a ring if and only if \((R,+)\) is an abelian group, multiplication \(\cdot\) is associative and has a multiplicative identity \(1\) and multiplication is left and right distributive with respect to addition.
\((\mathbb Z, +, \cdot)\) is a well known infinite ring which is commutative. The rational, real and complex numbers are other infinite commutative rings. Those are in fact fields as every non-zero element have a multiplicative inverse.
For a field \(F\) (finite or infinite), the polynomial ring \(F[X]\) is another example of infinite commutative ring.
Also for \(n\) integer, the integers modulo n is a finite ring that is commutative. Finally, according to Wedderburn theorem every finite division ring is commutative.
So what are examples of non commutative rings? Let’s provide a couple. Continue reading Non commutative rings
Database of Ring Theory
You want to find rings having some properties but not having other properties? Go there: Database of Ring Theory! A great repository of rings, their properties, and more ring theory stuff.
A simple ring which is not a division ring
Let’s recall that a simple ring is a non-zero ring that has no two-sided ideal besides the zero ideal and itself. A division ring is a simple ring. Is the converse true? The answer is negative and we provide here a counterexample of a simple ring which is not a division ring.
We prove that for \(n \ge 1\) the matrix ring \(M_n(F)\) of \(n \times n\) matrices over a field \(F\) is simple. \(M_n(F)\) is obviously not a division ring as the matrix with \(1\) at position \((1,1)\) and \(0\) elsewhere is not invertible.
Let’s prove first following lemma. Continue reading A simple ring which is not a division ring
Unique factorization domain that is not a Principal ideal domain
In this article, we provide an example of a unique factorization domain – UFD that is not a principal ideal domain – PID. However, it is known that a PID is a UFD.
We take a field \(F\), for example \(\mathbb Q\), \(\mathbb R\), \(\mathbb F_p\) (where \(p\) is a prime) or whatever more exotic.
The polynomial ring \(F[X]\) is a UFD. This follows from the fact that \(F[X]\) is a Euclidean domain. It is also known that for a UFD \(R\), \(R[X]\) is also a UFD. Therefore the polynomial ring \(F[X_1,X_2]\) in two variables is a UFD as \(F[X_1,X_2] = F[X_1][X_2]\). However the ideal \(I=(X_1,X_2)\) is not principal. Let’s prove it by contradiction.
Suppose that \((X_1,X_2) = (P)\) with \(P \in F[X_1,X_2]\). Then there exist two polynomials \(Q_1,Q_2 \in F[X_1,X_2]\) such that \(X_1=PQ_1\) and \(X_2=PQ_2\). As a polynomial in variable \(X_2\), the polynomial \(X_1\) is having degree \(0\). Therefore, the degree of \(P\) as a polynomial in variable \(X_2\) is also equal to \(0\). By symmetry, we get that the degree of \(P\) as a polynomial in variable \(X_1\) is equal to \(0\) too. Which implies that \(P\) is an element of the field \(F\) and consequently that \((X_1,X_2) = F[X_1,X_2]\).
But the equality \((X_1,X_2) = F[X_1,X_2]\) is absurd. Indeed, the degree of a polynomial \(X_1 T_1 + X_2 T_2\) cannot be equal to \(0\) for any \(T_1,T_2 \in F[X_1,X_2]\). And therefore \(1 \notin F[X_1,X_2]\).