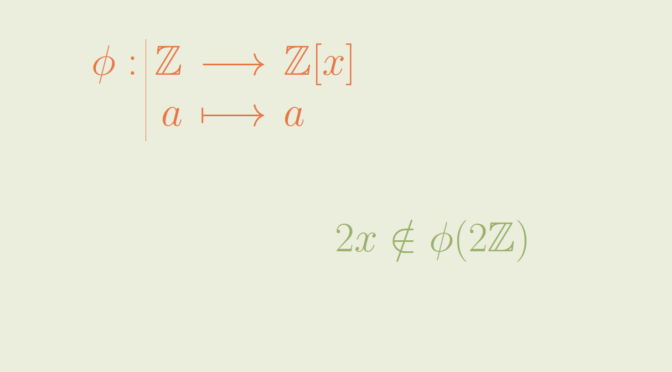If \(\phi : A \to B\) is a ring homomorphism then the image of a subring \(S \subset A\) is a subring \(\phi(A) \subset B\). Is the image of an ideal under a ring homomorphism also an ideal? The answer is negative. Let’s provide a simple counterexample.

Let’s take \(A=\mathbb Z\) the ring of the integers and for \(B\) the ring of the polynomials with integer coefficients \(\mathbb Z[x]\). The inclusion \(\phi : \mathbb Z \to \mathbb Z[x]\) is a ring homorphism. The subset \(2 \mathbb Z \subset \mathbb Z\) of even integers is an ideal. However \(2 \mathbb Z\) is not an ideal of \(\mathbb Z[x]\) as for example \(2x \notin 2\mathbb Z\).