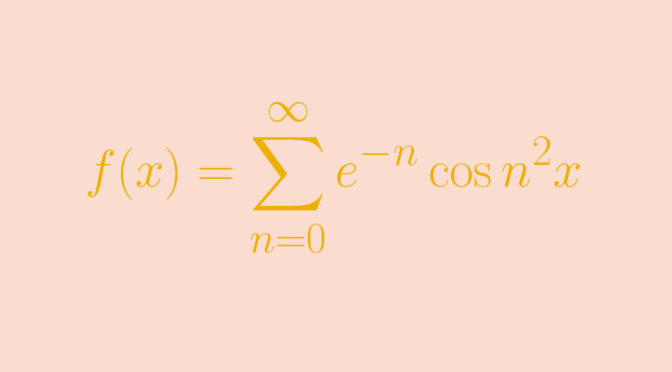Let’s describe a real function \(f\) whose Maclaurin series converges only at zero. For \(n \ge 0\) we denote \(f_n(x)= e^{-n} \cos n^2x\) and \[
f(x) = \sum_{n=0}^\infty f_n(x)=\sum_{n=0}^\infty e^{-n} \cos n^2 x.\] For \(k \ge 0\), the \(k\)th-derivative of \(f_n\) is \[
f_n^{(k)}(x) = e^{-n} n^{2k} \cos \left(n^2 x + \frac{k \pi}{2}\right)\] and \[
\left\vert f_n^{(k)}(x) \right\vert \le e^{-n} n^{2k}\] for all \(x \in \mathbb R\). Therefore \(\displaystyle \sum_{n=0}^\infty f_n^{(k)}(x)\) is normally convergent and \(f\) is an indefinitely differentiable function with \[
f^{(k)}(x) = \sum_{n=0}^\infty e^{-n} n^{2k} \cos \left(n^2 x + \frac{k \pi}{2}\right).\] Its Maclaurin series has only terms of even degree and the absolute value of the term of degree \(2k\) is \[
\left(\sum_{n=0}^\infty e^{-n} n^{4k}\right)\frac{x^{2k}}{(2k)!} > e^{-2k} (2k)^{4k}\frac{x^{2k}}{(2k)!} > \left(\frac{2kx}{e}\right)^{2k}.\] The right hand side of this inequality is greater than \(1\) for \(k \ge \frac{e}{2x}\). This means that for any nonzero \(x\) the Maclaurin series for \(f\) diverges.