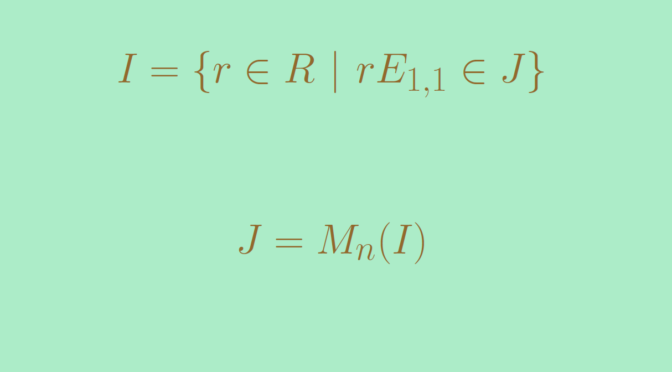Let’s recall that a simple ring is a non-zero ring that has no two-sided ideal besides the zero ideal and itself. A division ring is a simple ring. Is the converse true? The answer is negative and we provide here a counterexample of a simple ring which is not a division ring.
We prove that for \(n \ge 1\) the matrix ring \(M_n(F)\) of \(n \times n\) matrices over a field \(F\) is simple. \(M_n(F)\) is obviously not a division ring as the matrix with \(1\) at position \((1,1)\) and \(0\) elsewhere is not invertible.
Let’s prove first following lemma.
Lemma. For a commutative ring \(R\), every two-sided ideal of \(M_n(R)\) is of the form \(M_n(I)\) for a two-sided ideal \(I\) of \(R\).
Let \(J \subseteq M_n(R)\) be a two-sided ideal. Let \(E_{i,j}\) be the matrix with \(1\) at position \((i,j)\) and \(0\) elsewhere. Recall that matrices \(E_{i,j}\) satisfy the relations
\begin{gather*}
E_{i,j}E_{j,k} = E_{i,k}\\
E_{i,j}E_{l,k} = 0 \text{ for } j \neq l
\end{gather*} and for a matrix \(A=(a_{i,j})\), we have \[
E_{m,i}AE_{j,k}= a_{i,j}E_{m,k}\] Now let \[
I=\{r \in R \ | \ r E_{1,1} \in J\}\] \(I\) is a two-sided ideal of \(R\). Indeed, let \(a \in R\) and \(r \in I\). We have \((a E_{1,1})(r E_{1,1}) = ar E_{1,1}\) hence \(ar \in I\). Similarly, \(ra \in I\).
For any matrix \(A \in J\) we have \[
a_{i,j} E_{1,1} = E_{1,i} A E_{j,1}\] As \(J\) is an ideal, the right hand side belongs to \(J\) and hence \(a_{i,j} \in I\). It follows that \(J \subseteq M_n(I)\). Conversely an element \(A \in M_n(I)\) is a sum of elements of the form \(r E_{i,j}\) with \(r \in I\). The equality \(E_{i,1} (r E_{1,1} ) E_{1,j} = r E_{i,j}\) implies that \(r E_{i,j} \in J\) for \(r \in I\). Therefore \(A \in J\) and we have proven \(J=M_n(I)\).
For a field \(F\), we can easily conclude with the lemma that \(M_n(F)\) is a simple ring as the only ideals of a field \(F\) are \(\{0\}\) and the field \(F\) itself.