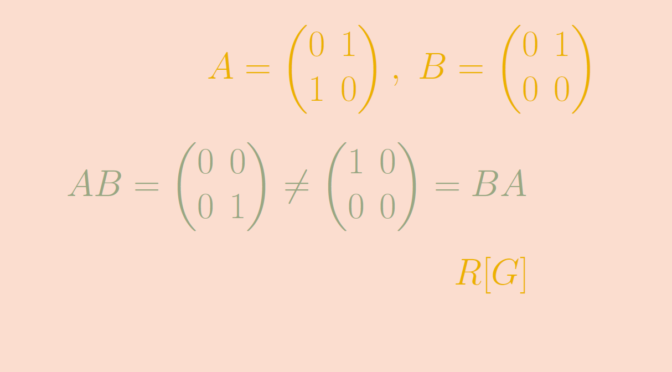Let’s recall that a set \(R\) equipped with two operations \((R,+,\cdot)\) is a ring if and only if \((R,+)\) is an abelian group, multiplication \(\cdot\) is associative and has a multiplicative identity \(1\) and multiplication is left and right distributive with respect to addition.
\((\mathbb Z, +, \cdot)\) is a well known infinite ring which is commutative. The rational, real and complex numbers are other infinite commutative rings. Those are in fact fields as every non-zero element have a multiplicative inverse.
For a field \(F\) (finite or infinite), the polynomial ring \(F[X]\) is another example of infinite commutative ring.
Also for \(n\) integer, the integers modulo n is a finite ring that is commutative. Finally, according to Wedderburn theorem every finite division ring is commutative.
So what are examples of non commutative rings? Let’s provide a couple.
Matrix rings
Consider a field \(F\) and an integer \(n \ge 2\). The set \(M_n(F)\) of square matrices over the field \(F\) is a ring. \(M_n(F)\) is never commutative. Indeed, given the matrices \[
A=\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}, \ B=\begin{pmatrix}
0 & 1 \\
0 & 0
\end{pmatrix},\] we have \[
AB= \begin{pmatrix}
0 & 0 \\
0 & 1
\end{pmatrix} \neq
\begin{pmatrix}
1 & 0 \\
0 & 0
\end{pmatrix} = BA.\]
Therefore with matrix rings we get examples of non-commutative rings that can be finite or infinite depending on whether \(F\) is finite or not. One can notice that \(M_n(F)\) is never a division ring as \(B^2=0\). Consequently \(B\) cannot have a multiplicative inverse.
Group rings
Considering a group \(G\) and a ring \(R\). The group ring of \(G\) over \(R\), denoted by \(R[G]\) is the set of mappings \(f : G \to R\) with finite support, i.e. taking a finite number of non-zero values. The addition of two elements \(f,g \in R[G]\) is the mapping \(f+g: x \mapsto f(x)+g(x)\). The product is the mapping \[
f \cdot g : x \mapsto \sum_{uv=x} f(u) g(v) = \sum_{u \in G} f(u)g(u^{-1}x)\] which is well defined because \(f,g\) are of finite support.
One can verify that \(R[G]\) is indeed a ring.
When \(G\) is a non-commutative group, \(R[G]\) is a non-commutative ring as for \(r,s \in G\) such that \(rs \neq sr\) we have \(\mathbf 1_{rs} \neq \mathbf 1_{sr}\). Where for \(g \in G\), \(\mathbf 1_{g} \in R[G]\) denotes the finite support function that maps \(g\) to \(1\) and all the other elements to \(0\).