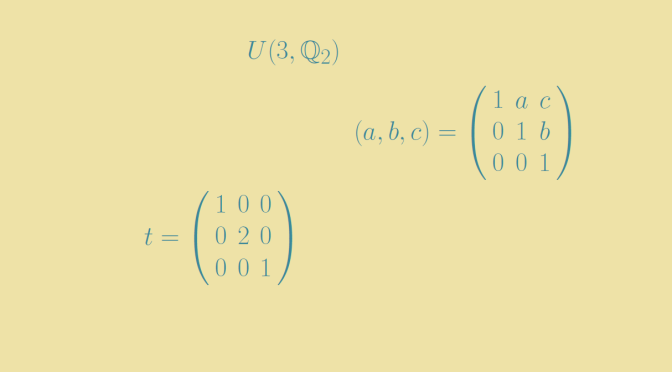Let \(\mathbb{Q}_2\) be the ring of rational numbers of the form \(m2^n\) with \(m, n \in \mathbb{Z}\) and \(N = U(3, \mathbb{Q}_2)\) the group of unitriangular matrices of dimension \(3\) over \(\mathbb{Q}_2\). Let \(t\) be the diagonal matrix with diagonal entries: \(1, 2, 1\) and put \(H = \langle t, N \rangle\). We will prove that \(H\) is finitely generated and that one of its quotient group \(G\) is isomorphic to a proper quotient group of \(G\).
Denote by \((a, b, c)\) the unitriangular matrix \[1 + aE_{12} + bE_{23} + cE_{13}=\left( \begin{array}{ccc}
1 & a & c \\
0 & 1 & b \\
0 & 0 & 1 \end{array} \right)\] and write \(u = (1, 0, 0)\), \(v = (0, 1, 0)\), \(w = (0, 0, 1)\).
\(H = \langle t,u,v \rangle\) and therefore \(H\) is finitely generated
The inclusion \(\langle t,u,v \rangle \subseteq H\) is obvious. In order to prove the reverse inclusion it is sufficient to prove that \(N \subseteq \langle t,u,v \rangle\). Now for \(m,n \in \mathbb{Z}\) we have:
\[t^{-n}u^mt^n=\left( \begin{array}{ccc}
1 & m2^n & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \end{array} \right) \mbox{ and } t^{n}v^mt^{-n}=\left( \begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & m2^n \\
0 & 0 & 1 \end{array} \right)\] which proves that for \(a,b \in \mathbb{Q}_2\), \((a,0,0)\) and \((0,b,0)\) belong to \(\langle t,u,v \rangle\).
Also for \(c \in \mathbb{Q}_2\) the commutator \([u,(0,c,0)]\) is equal to \((0,0,c)\). Finally for \(a,b,c \in \mathbb{Q}_2\) we have: \((a,b,c)=(0,0,c)(0,b,0)(a,0,0)\) leading us to the desired conclusions \(N \subseteq \langle t,u,v \rangle\) and \(H = \langle t,u,v \rangle\).
The group \(G=H/\langle w^2 \rangle\) is finitely generated and isomorphic to \(\overline{G}=H/\langle w \rangle\)
For \(c \in \mathbb{Q}_2\) one can notice that:
- for all \(n \in \mathbb{Z}\): \((0,0,c)^n = (0,0,nc)\),
- \((0,0,c)\) commutes with all elements in \(H\).
Therefore for all \(c \in \mathbb{Q}_2\), \(\langle (0,0,c) \rangle\) is a normal subgroup of \(H\), allowing us to define in particular \(G=H/\langle w^2 \rangle\) and \(\overline{G}=H/\langle w \rangle\).
One can show that the assignments \(\varphi: (a,b,c) \mapsto (a,2b,2c)\) and \(\varphi: t \mapsto t\) determine an automorphism of \(H\). We have \(\varphi(\langle w \rangle) = \langle w^2 \rangle\) and if we denote \(p: H \mapsto H/\langle w^2 \rangle\) the canonical homomorphism, \(p \circ \varphi\) is an epimorphism from \(H\) to \(H/\langle w^2 \rangle\) whose kernel is \(\langle w \rangle\). Therefore \(\overline{G} = H/\langle w\rangle \simeq H/\langle w^2 \rangle=G\).
\(\langle w \rangle\) is a normal subgroup of \(H\) which contains \(\langle w^2 \rangle\). By the third isomorphism theorem of groups we get:
\[G \simeq H/\langle w \rangle \simeq (H/\langle w^2 \rangle)/(\langle w \rangle/\langle w^2 \rangle)
\simeq G/(\langle w \rangle/\langle w^2 \rangle)\] \(\langle w \rangle\) is an infinite cyclic group and \(\langle w \rangle/\langle w^2 \rangle \simeq \mathbb{Z}_2\) which proves that \(G/(\langle w \rangle/\langle w^2 \rangle)\) is a proper quotient group of \(G\) and that \(G\) is not hopfian.
Finally we conclude with the proof of \(G\) solubility by considering \(H\) derived series. One can verify that \(H^\prime \subseteq N\), \(H^{(2)} \subseteq N^\prime=\{(0,0,c) ; c \in\mathbb{Q}_2\}\) and \(H^{(3)} = \textbf{1}\) which proves that \(H\) is soluble. \(G\) which is isomorphic to a quotient group of \(H\) is therefore also soluble.
This example of a finitely generated soluble non hopfian group is from the mathematician Philip Hall.