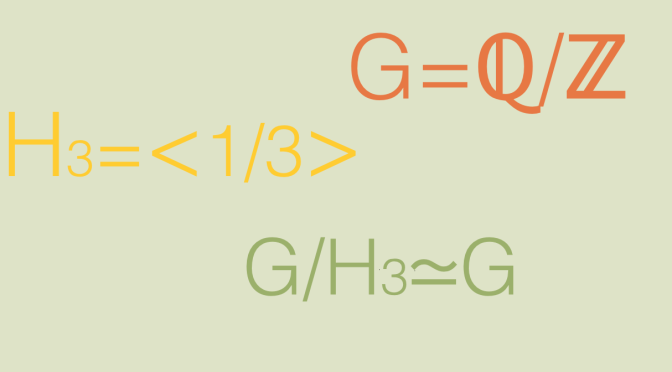The basic question that we raise here is the following one: given a group \(G\) and a proper subgroup \(H\) (i.e. \(H \notin \{\{1\},G\}\), can \(G/H\) be isomorphic to \(G\)? A group \(G\) is said to be hopfian (after Heinz Hopf) if it is not isomorphic with a proper quotient group.

All finite groups are hopfian as \(|G/H| = |G| \div |H|\). Also, all simple groups are hopfian as a simple group doesn’t have proper subgroups.

So we need to turn ourselves to infinite groups to uncover non hopfian groups.

The group \(G_1=\bigoplus\limits_{i=1}^\infty\ \mathbb Z\)

The group \(G_1\) is an additive group and \(H_1=\mathbb Z\ \oplus\ \bigoplus\limits_{i=2}^\infty\ 0
\) is a proper subgroup. As \(G_1\) is commutative, \(H_1\) is normal in \(G_1\) (\(H_1 \triangleleft G_1\)). For \(x=(x_1,x_2, \dots) \in G_1\) we define \(\varphi(x)=(x_2,x_3, \dots) \in G_1\). Taking \(x=(x_1,x_2, \dots),y=(y_1,y_2, \dots) \in G_1\) we notice that:

• \(\varphi(x+y)=\varphi(x)+\varphi(y)\),
• \(\varphi(-x)=-\varphi(x)\),
• the value of \(\varphi\) is constant on each class of \(G_1/H_1\).

enabling to define a morphism \(\overline{\varphi}: G_1/H_1 \rightarrow G_1\) which one can verify to be an isomorphism.

The group \(G_2=(\mathbb{Q}/\mathbb{Z}, +)\)

We take an integer \(n \ge 2\) and denote by \(a \in G_2\) the equivalence class of \(\frac{1}{n}\). The order of \(a\) is equal to \(n\). Let’s consider the function:
\[\begin{array}{l|rcl}
\varphi_n : & G_2 & \longrightarrow & G_2 \\
& x & \longmapsto & n \cdot x\end{array}\]
As \(G_2\) is commutative, \(\varphi_n\) is a morphism. One can verify that \(\ker \varphi_n = H_n\) where \(H_n\) is the subgroup of \(G_2\) generated by \(a\). Moreover \(\varphi_n\) is onto as for a representative \(p/q\) of an element of \(\mathbb{Q}/\mathbb{Z}\), \(p/(nq)\) is pre-image of \(p/q\). Finally by the first isomorphism theorem of groups, we can define an isomorphism \(\varphi_n: G_2/H_n \rightarrow G_2\).

The groups \(G_1\) and \(G_2\) defined above are not finitely generated. I’ll come back later on with an example of a finitely generated group isomorphic to a proper quotient group.