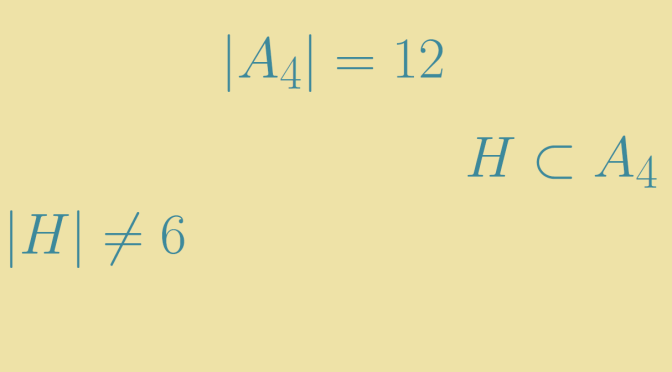Lagrange’s theorem, states that for any finite group \(G\), the order (number of elements) of every subgroup \(H\) of \(G\) divides the order of \(G\) (denoted by \(\vert G \vert\)).

Lagrange’s theorem raises the converse question as to whether every divisor \(d\) of the order of a group is the order of some subgroup. According to Cauchy’s theorem this is true when \(d\) is a prime.

However, this does not hold in general: given a finite group \(G\) and a divisor \(d\) of \(\vert G \vert\), there does not necessarily exist a subgroup of \(G\) with order \(d\). The alternating group \(G = A_4\), which has \(12\) elements has no subgroup of order \(6\). We prove it below.

\(G\) consists of:

• The identity or neutral element \(e\).
• The three elements that are product of disjoint transpositions. Those \(3\) elements with \(e\) make up a subgroup \(V \subset H\) (\(V\) is isomorphic to the Klein four-group)
• The eight 3-cycles.

Suppose that \(H \subset G\) is a subgroup of order \(6\) and that \(H^\prime\) denotes the intersection \(H \cap V\). \(H^\prime\) is a subgroup of \(H\) and \(V\). By Lagrange’s theorem, \(H^\prime\) order divides \(4\) and \(6\). So \(\vert H^\prime \vert\) is equal to \(1\) or to \(2\). If \(\vert H^\prime \vert=1\), the map \((h,v) \mapsto h \cdot v\) defined from \(H \times V\) to \(G\) is one-to-one. Which doesn’t make sense as \(G\) would have at least \(24\) elements. Therefore \(\vert H^\prime \vert=2\) and \(H\) is made up the identity \(e\), an element \(v\) which is product of two disjoint transpositions and six 3-cycles.

Also the index \(\vert G : H\vert\) is equal to \(2\) and consequently \(H\) is a normal subgroup of \(G\). We recall the argument. For \(a \in G \setminus H\) the left cosets \(H, aH\) form a partition of \(G\). Similarly, the right cosets \(H, Ha\) form a partition of \(G\). As \(aH \neq H\), we have \(aH =Ha\) which allows to conclude.

We denote \(v=(i,j)(k,l)\) with \(\{i,j,k,l\} = \{1,2,3,4\}\) and \(t\) the 3-cycle \((i,j,k)\). We have \(tvt^{-1}=(j,k)(i,l) \neq (i,j)(k,l)\) and \(tvt^{-1} \in H\) as \(H \triangleleft G\). In contradiction with the cardinality of \(\vert H^\prime \vert = \vert H \cap V \vert= 2\). We have finally proven that \(A_4\) has no subgroup of order \(6\).