Introduction on total variation of functions

Recall that a function of bounded variation, also known as a BV-function, is a real-valued function whose total variation is bounded (finite).

Being more formal, the total variation of a real-valued function \(f\), defined on an interval \([a,b] \subset \mathbb{R}\) is the quantity:
\[V_a^b(f) = \sup\limits_{P \in \mathcal{P}} \sum_{i=0}^{n_P-1} \left\vert f(x_{i+1}) – f(x_i) \right\vert\] where the supremum is taken over the set \(\mathcal{P}\) of all partitions of the interval considered.

First example of a function which is not of bounded variation

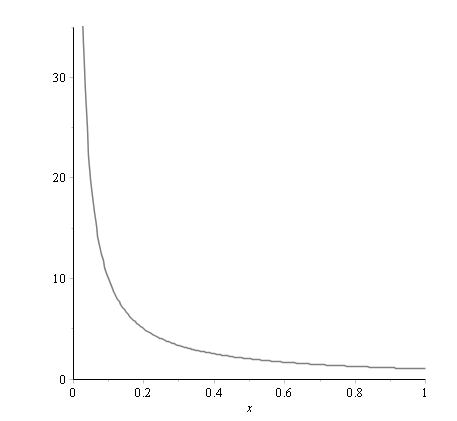It is easy to show a function that is not of bounded variation. Consider the function \(f\) defined on the interval \([0,1]\) by:
\[f(x)=\left\{
\begin{array}{ll}
0 & \mbox{if } x=0\\
\frac{1}{x} & \mbox{if } x \in (0,1]\\
\end{array}
\right.\]
For \(0 < u < 1\), we have \(V_0^1(f) > V_u^1(f) = \frac{1}{u} – 1\) and taking \(u\) as small as desired we get \(V_0^1(f) = +\infty\). The function \(f\) is not bounded on its domain.

A bounded function which is not of bounded variation

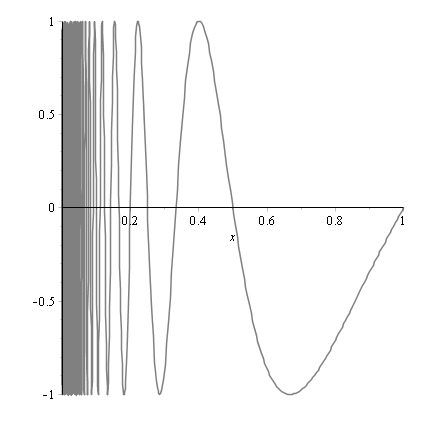Can a bounded function not be of bounded variation? The answer is also positive as proven by taking \(g\) defined on the interval \([0,1]\) by:
\[g(x)=\left\{
\begin{array}{ll}
0 & \mbox{if } x=0\\
\sin(\frac{\pi}{x}) & \mbox{if } x \in (0,1]\\
\end{array}
\right.\]
For an integer \(p \ge 1\), we have \(V_0^1(g) > V_{\frac{1}{2p+1/2}}^{\frac{2}{5}}(g) = 4(p-1)\) and therefore \(V_0^1(g) = +\infty\).

A continuous function which is not of bounded variation

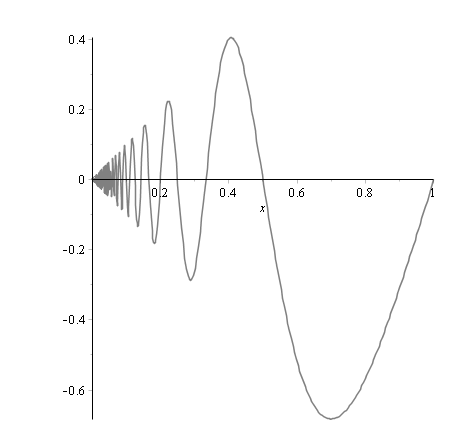And finally we prove that the function \(h\) defined on the interval \([0,1]\) by:
\[h(x)=
\left\{
\begin{array}{ll}
0 & \mbox{if } x=0\\
x \sin(\frac{\pi}{x}) & \mbox{if } x \in (0,1]\\
\end{array}
\right.\]
is continuous and not of bounded variation. Indeed \(h\) is continuous at \(x \neq 0\) as it is the product of two continuous functions at that point. \(h\) is also continuous at \(0\) because \(|h(x)| \le x\) for \(x \in [0,1]\). We now consider the total variation of \(h\). For \(2 \le p\) integer, we have \(V_0^1(h) \ge V_{\frac{1}{2p+1/2}}^{\frac{2}{5}}(h)\) as \([\frac{1}{2p+1/2},\frac{2}{5}] \subset [0,1]\). Taking \(\{\frac{1}{2p+1/2},\frac{1}{2p-1/2},\frac{1}{2p-3/2},\dots,\frac{1}{2+1/2}=\frac{2}{5}\}\) as a partition of \([\frac{1}{2p+1/2},\frac{2}{5}]\), one can prove that \(V_{\frac{1}{2p+1/2}}^{\frac{2}{5}}(h) \ge 2\sum_{i=1}^{p-1} \frac{1}{i+2}\). As the last series diverges, \(h\) is not of bounded variation.