Introduction to ordered fields
Let \(K\) be a field. An ordering of \(K\) is a subset \(P\) of \(K\) having the following properties:
- ORD 1
- Given \(x \in K\), we have either \(x \in P\), or \(x=0\), or \(-x \in P\), and these three possibilities are mutually exclusive. In other words, \(K\) is the disjoint union of \(P\), \(\{0\}\), and \(-P\).
- ORD 2
- If \(x, y \in P\), then \(x+y\) and \(xy \in P\).
We shall also say that \(K\) is ordered by \(P\), and we call \(P\) the set of positive elements.
Let’s notice following properties of an ordered field:
- Since \(1 \neq 0\) and \(1=1^2=(-1)^2\) we see that \(1 \in P\).
- More generally, a non zero square is always positive because for \(x \neq 0\), \(x^2=(-x)^2\) and either \(x \in P\) or \(-x \in P\).
A finite field cannot be ordered
Let us assume that \(K\) is ordered by \(P\). By ORD 2, it follows that \(p= 1+ \cdots + 1 \in P\), whence \(K\) has characteristic \(0\) and therefore cannot be finite.
\(\mathbb{Q}\) is an infinite ordered field
One can verify at once that \(\mathbb{Q}\) is ordered by taking for \(P\) the set of positive rational numbers.
This is the only possible ordering of \(\mathbb{Q}\). Suppose that \(\mathbb{Q}\) is ordered by \(T\). We have seen above that \(1 \in T\). Therefore \(n=1 + \cdots +1 \in P\), i.e. \(\mathbb{N^*} \subset T\).
If \(m\) is a positive integer, \(\frac{1}{m}=m \cdot \frac{1}{m^2} \in T\) by ORD 2 and consequently \(\mathbb{Q}^*_+ \subset T\). A negative rational cannot belong to \(T\) because \(0\) would also belong to \(T\) in contradiction with ORD 1. Finally \(T=\mathbb{Q}^*_+\).
\(\mathbb{C}\) is an infinite field that cannot be ordered
While \(\mathbb{Q}\) is an ordered field included in \(\mathbb{C}\), \(\mathbb{C}\) cannot be ordered. To show that this is the case, assume that \(\mathbb{C}\) is ordered by a subset \(P\). If \(\imath \in P\), then by ORD 2, \(\imath^2 = -1 \in P\) and \(\imath^4 = 1 \in P\). Still according to ORD 2, \(\imath^2 + \imath^4=0 \in P\) contradicting ORD 1. And if \(-\imath \in P\), we have the same contradiction as before because \((-\imath)^2 = \imath^2\).

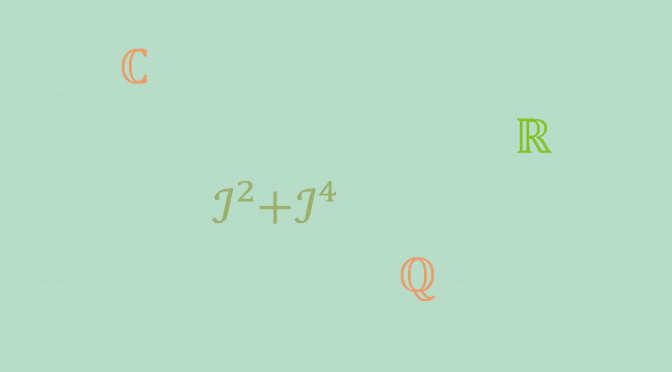
One thought on “An infinite field that cannot be ordered”