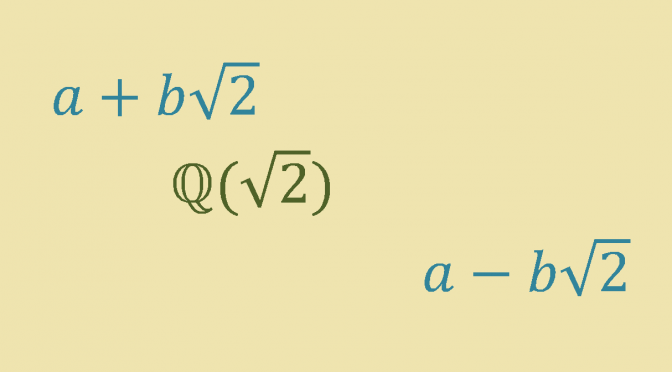For a short reminder about ordered fields you can have a look to following post. We prove there that \(\mathbb{Q}\) can be ordered in only one way.

That is also the case of \(\mathbb{R}\) as \(\mathbb{R}\) is a real-closed field. And one can prove that the only possible positive cone of a real-closed field is the subset of squares.

However \(\mathbb{Q}(\sqrt{2})\) is a subfield of \(\mathbb{R}\) that can be ordered in two distinct ways.

First \(\mathbb{Q}(\sqrt{2})\) can be ordered using the induced order from \(\mathbb{R}\) which means selecting as the positive cone the set \(P_0=\mathbb{Q}(\sqrt{2}) \cap \mathbb{R_+^*}\). With this order, an element \(a+b\sqrt{2} \in \mathbb{Q}(\sqrt{2})\) is positive when \(a+b\sqrt{2} \in \mathbb{R_+^*}\).

However \(\mathbb{Q}(\sqrt{2})\) can be ordered in a second way. The map:
\(\begin{array}{l|rcl}
\varphi : & \mathbb{Q}(\sqrt{2}) & \longrightarrow & \mathbb{Q}(\sqrt{2}) \\
& a+b\sqrt{2} & \longmapsto & a-b\sqrt{2} \end{array}\)
is a field isomorphism. Consider:
\[P=\{a+b\sqrt{2} ; a,b \in \mathbb{Q} \mbox{ and } a-b\sqrt{2} \in \mathbb{R_+^*}\} = \varphi^{-1}(P_0)\]One can verify that \(P\) is an ordering of \(\mathbb{Q}(\sqrt{2})\):

• Clearly \(\mathbb{Q}(\sqrt{2})\) is the disjoint union of \(P\), \(\{0\}\) and \(-P\).
• \(P+P = \varphi^{-1}(P_0)+\varphi^{-1}(P_0)=\varphi^{-1}(P_0+P_0) \subset \varphi^{-1}(P_0)=P\)
• \(P \cdot P = \varphi^{-1}(P_0) \cdot \varphi^{-1}(P_0)=\varphi^{-1}(P_0 \cdot P_0) \subset \varphi^{-1}(P_0)=P\)

It can also be proven that there is no other ordering of \(\mathbb{Q}(\sqrt{2})\) than the two mentioned above with:

• \(P=\{a+b\sqrt{2} ; a,b \in \mathbb{Q} \mbox{ and } a+b\sqrt{2} > 0\}\) if \(\sqrt{2} \in P\).
• \(P=\{a+b\sqrt{2} ; a,b \in \mathbb{Q} \mbox{ and } a-b\sqrt{2} > 0\}\) if \(-\sqrt{2} \in P\).

The proof is based on the equation \((a+b\sqrt{2})(a-b\sqrt{2})=a^2-2b^2\), the fact that \(\mathbb{Q}^*_+ \subset P\) and a case by case analysis based on the signs of \(a\) and \(b\).