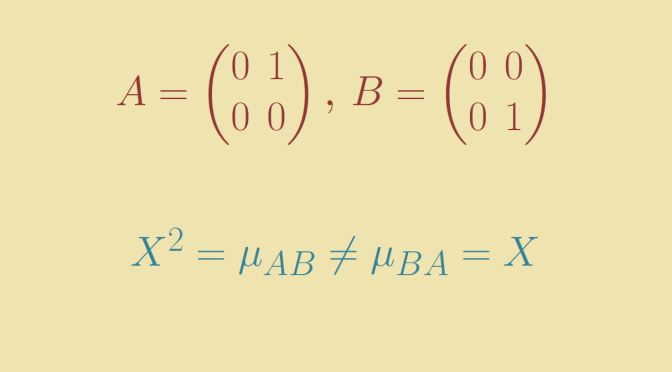We consider here the algebra of matrices \(\mathcal{M}_n(\mathbb F)\) of dimension \(n \ge 1\) over a field \(\mathbb F\).

It is well known that for \(A,B \in \mathcal{M}_n(\mathbb F)\), the characteristic polynomial \(p_{AB}\) of the product \(AB\) is equal to the one (namely \(p_{BA}\)) of the product of \(BA\). What about the minimal polynomial?

Unlikely for the characteristic polynomials, the minimal polynomial \(\mu_{AB}\) of \(AB\) maybe different to the one of \(BA\).

Consider the two matrices \[
A=\begin{pmatrix}
0 & 1\\
0 & 0\end{pmatrix} \text{, }
B=\begin{pmatrix}
0 & 0\\
0 & 1\end{pmatrix}\] which can be defined whatever the field we consider: \(\mathbb R, \mathbb C\) or even a field of finite characteristic.

One can verify that \[
AB=A=\begin{pmatrix}
0 & 1\\
0 & 0\end{pmatrix} \text{, }
BA=\begin{pmatrix}
0 & 0\\
0 & 0\end{pmatrix}\]

As \(BA\) is the zero matrix, its minimal polynomial is \(\mu_{BA}=X\). Regarding the one of \(AB\), we have \((AB)^2=A^2=0\) hence \(\mu_{AB}\) divides \(X^2\). Moreover \(\mu_{AB}\) cannot be equal to \(X\) as \(AB \neq 0\). Finally \(\mu_{AB}=X^2\) and we verify that \[X^2=\mu_{AB} \neq \mu_{BA}=X.\]