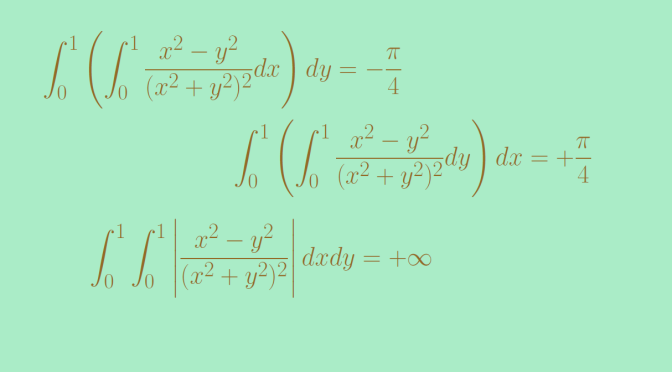We present here some counterexamples around the Fubini theorem.
We recall Fubini’s theorem for integrable functions:
let \(X\) and \(Y\) be \(\sigma\)-finite measure spaces and suppose that \(X \times Y\) is given the product measure. Let \(f\) be a measurable function for the product measure. Then if \(f\) is \(X \times Y\) integrable, which means that \(\displaystyle \int_{X \times Y} \vert f(x,y) \vert d(x,y) < \infty\), we have \[\int_X \left( \int_Y f(x,y) dy \right) dx = \int_Y \left( \int_X f(x,y) dx \right) dy = \int_{X \times Y} f(x,y) d(x,y)\]
Let's see what happens when some hypothesis of Fubini's theorem are not fulfilled.
The case of a measure that is not \(\sigma\)-finite
We take the set \(I=[0,1]\) equipped on one side with the Borel set and Lebesgue measure \(\lambda\) for \(X\) and on the other side the same set \(I=[0,1]\) equipped with the power set and the counting measure \(m\) for \(Y\).
The diagonal set \(\Delta=\{(x,x) \ : \ x \in [0,1] \}\) is a closed subset of \(I^2\). Hence \[\Delta \in \mathcal{B}(I^2) = \mathcal{B}(I) \times \mathcal{B}(I) \subset \mathcal{B}(I) \times \mathcal{P}(I).\]
Therefore, the characteristic map \(\mathbf{1}_{\Delta}\) is measurable for the measure induced on \(X \times Y\). However, we have on one side
\begin{align*}
\int_I \left( \int_I \mathbf{1}_{\Delta}(x,y) dm(y) \right) d\lambda(x) &= \int_I \left( \int_I \mathbf{1}_{\{x\}}(y) dm(y) \right) d\lambda(x)\\
&= \int_I m(\{x\}) d\lambda(x) = \lambda(I)=1
\end{align*}
and on the other side
\begin{align*}
\int_I \left( \int_I \mathbf{1}_{\Delta}(x,y) d\lambda(x) \right) dm(y) &= \int_I \left( \int_I \mathbf{1}_{\{y\}}(x) d\lambda(x) \right) dm(y)\\
&= \int_I \lambda(\{y\}) dm(y) = \int_I 0 \ dm(y)=0
\end{align*}
Those two integrals are different. This is not contradicting Fubini’s theorem as the counting measure on \(I=[0,1]\) is not \(\sigma\)-finite. Indeed, a countable union of finite measure subsets for the counting measure is at most countable while \(I\) has the cardinality of the continuum.
The case of a non-integrable function for the product measure
Let’s consider for \(X\) and \(Y\) the segment \(I=[0,1]\) equipped with the Borel set \(\mathcal{B}(I)\) and the Lebesgue measure. The function \[f(x,y)=\frac{x^2-y^2}{(x^2+y^2)^2}.\] \(f\) is continuous on \(I \times I\) except at the origin, hence is measurable.
We have \[\int_0^1 \frac{x^2-y^2}{(x^2+y^2)^2} dy = \left[ \frac{y}{x^2+y^2} \right]_{y=0}^1=\frac{1}{1+x^2}\] and \[\int_0^1 \left(\int_0^1 \frac{x^2-y^2}{(x^2+y^2)^2} dy \right) dx = \int_0^1 \frac{1}{1+x^2} dx = \frac{\pi}{4}\] Proceeding to the integral computation in the opposite order we get \[\int_0^1 \left(\int_0^1 \frac{x^2-y^2}{(x^2+y^2)^2} dx \right) dy = – \frac{\pi}{4}.\]
Let’s have a look to \(\displaystyle \int_{I \times I} \vert f(x,y) \vert d(x,y)\). We have
\begin{align*}
\int_{I \times I} \left\vert \frac{x^2-y^2}{(x^2+y^2)^2} \right\vert d(x,y) &\ge \int_0^1 \left(\int_0^ x\frac{x^2-y^2}{(x^2+y^2)^2} dy \right) dx\\
&=\int_0^1 \left[ \frac{y}{x^2+y^2} \right]_{y=0}^x dx\\
&= \int_0^1 \frac{1}{2x} dx = + \infty
\end{align*} avoiding any contradiction with Fubini’s theorem.