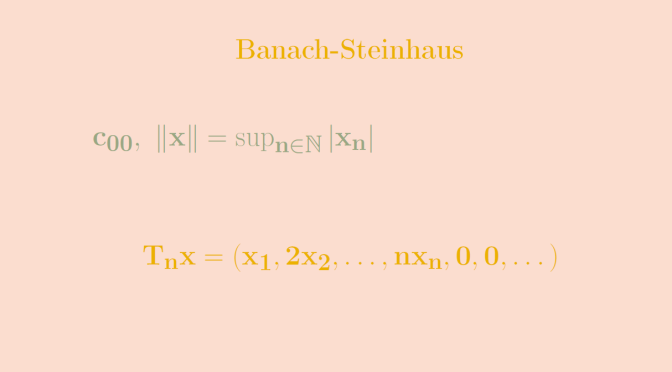In this article we look at what happens to Banach-Steinhaus theorem when the completness hypothesis is not fulfilled. One form of Banach-Steinhaus theorem is the following one.

Banach-Steinhaus Theorem Let \(T_n : E \to F\) be a sequence of continuous linear maps from a Banach space \(E\) to a normed space \(F\). If for all \(x \in E\) the sequence \(T_n x\) is convergent to \(Tx\), then \(T\) is a continuous linear map.

A sequence of continuous linear maps converging to an unbounded linear map

Let \(c_{00}\) be the vector space of real sequences \(x=(x_n)\) eventually vanishing, equipped with the norm \[\Vert x \Vert = \sup_{n \in \mathbb N} \vert x_n \vert\] For \(n \in \mathbb N\), \(T_n : E \to E\) denotes the linear map defined by \[T_n x = (x_1,2 x_2, \dots, n x_n,0,0, \dots).\] \(T_n\) is continuous as for \(\Vert x \Vert \le 1\), we have
\begin{align*}
\Vert T_n x \Vert &= \Vert (x_1,2 x_2, \dots, n x_n,0,0, \dots) \Vert\\
& = \sup_{1 \le k \le n} \vert k x_k \vert \le n \Vert x \Vert \le n
\end{align*}

For any \(x \in E\) there exists \(k \in \mathbb N\) such that \(x=(x_1, \dots , x_k, 0,0, \dots)\). Hence for \(n \ge k\), \(T_n x\) is constant and equal to \((x_1,2 x_2, \dots,k x_k,0,0, \dots)\), which proves that \((T_n x)\) converges.

However \((T_n)\) is not uniformly bounded as we can see looking at the elements \(\mathbf{1}_n \in E\) which have all terms equal to \(0\) except the first \(n\) ones which are equal to \(1\):\[\Vert \mathbf{1}_n \Vert = 1 \text{ and } \Vert T_n \mathbf{1}_n\Vert = \Vert (1,2, \dots, n, 0,0, \dots) \Vert = n.\] However, this does not contradict Banach-Steinhaus Theorem. \(E\) is not complete as we can see considering the sequence \((y_n)\) of \(E\) where \(y_n=(1, \frac{1}{2}, \dots, \frac{1}{n},0,0,\dots)\). \((y_n)\) is a Cauchy sequence as for \(1 \le p < q\): \(\Vert y_q-y_p \Vert=\frac{1}{p+1}\) but \((y_n)\) doesn't converges in \(E\).

A discontinuous bilinear map which is separately continuous

A corollary of Banach-Steinhaus Theorem is that if \(E\) is a Banach space and \(F\) a normed space, a bilinear map \(B : E \times E \to F\) which is separately continuous is continuous (as a map of two variables).

We prove here that it might not be the case when \(E\) is not complete. We take for \(E\) the vector space of the real polynomials \(\mathbb R[X]\) equipped with the norm \[\Vert P \Vert_1 = \int_0^1 \vert P(t) \vert dt, \ P \in \mathbb R[X]\] and for \(B\) the bilinear functional defined by \[B(P,Q) = \int_0^1 P(t) Q(t) dt, \ P,Q \in \mathbb R[X].\]

For \(P\) fixed we have for any \(Q \in \mathbb R[X]\)
\begin{align*}
\vert B(P,Q) \vert &= \left\vert \int_0^1 P(t) Q(t) dt \right\vert\\
& \le \left(\sup_{t \in [0,1]} \vert P(t) \vert \right) \int_0^1 \vert Q(t) \vert dt\\
&= \left(\sup_{t \in [0,1]} \vert P(t) \vert \right) \Vert Q \Vert_1
\end{align*} which proves that \(B\) is continuous for the second variable. \(B\) is also continuous for the first variable as it is symmetric.

Let’s prove that \(B\) is not continuous. We consider the sequence of polynomials \((P_n)\) defined for \(n \in \mathbb N\) by \(P_n(t)=n^{2/3} t^{n-1}\). Then \[\Vert P_n \Vert_1 = n^{2/3} \int_0^1 t^{n-1} dt = \frac{1}{n^{1/3}} \le 1\] while \[\vert B(P_n,P_n) \vert = \int_0^1 P_n^2(t) dt = \frac{n^{4/3}}{2n-1},\] allowing us to conclude as \(\lim\limits_{n \to \infty} \frac{n^{4/3}}{2n-1} = +\infty\) which proves that \(B\) is unbounded on the product of two unit balls.

As for the previous example, \(\mathbb R[X]\) is not complete. This can be proved considering the sequence of polynomials \((R_n)\) where \(\displaystyle R_n=\sum_{k=1}^n \frac{t^k}{k}\). For \(1 \le p < q\) we have \[\Vert R_q-R_p \Vert_1=\int_0^1 \left\vert \sum_{k=p+1}^q \frac{t^k}{k} \right\vert dt \le \frac{1}{p+1}\] Hence \((R_n)\) is a Cauchy sequence. However it doesn't converge to a polynomial.