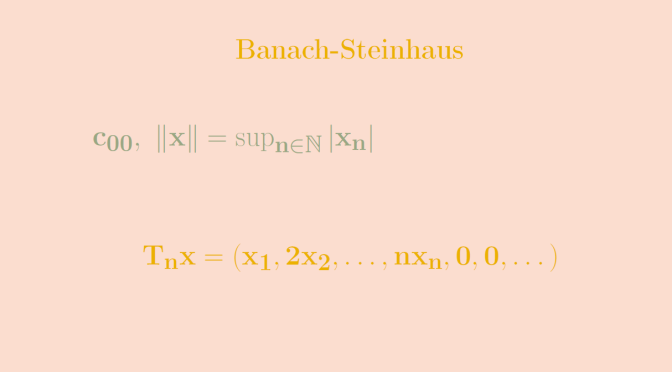In this article we look at what happens to Banach-Steinhaus theorem when the completness hypothesis is not fulfilled. One form of Banach-Steinhaus theorem is the following one.

Banach-Steinhaus Theorem Let \(T_n : E \to F\) be a sequence of continuous linear maps from a Banach space \(E\) to a normed space \(F\). If for all \(x \in E\) the sequence \(T_n x\) is convergent to \(Tx\), then \(T\) is a continuous linear map.

A sequence of continuous linear maps converging to an unbounded linear map

Let \(c_{00}\) be the vector space of real sequences \(x=(x_n)\) eventually vanishing, equipped with the norm \[\Vert x \Vert = \sup_{n \in \mathbb N} \vert x_n \vert\] For \(n \in \mathbb N\), \(T_n : E \to E\) denotes the linear map defined by \[T_n x = (x_1,2 x_2, \dots, n x_n,0,0, \dots).\] \(T_n\) is continuous as for \(\Vert x \Vert \le 1\), we have
\begin{align*}
\Vert T_n x \Vert &= \Vert (x_1,2 x_2, \dots, n x_n,0,0, \dots) \Vert\\
& = \sup_{1 \le k \le n} \vert k x_k \vert \le n \Vert x \Vert \le n
\end{align*} Continue reading Counterexamples around Banach-Steinhaus theorem →