Definition of the Cantor set

The Cantor ternary set (named Cantor set below) \(K\) is a subset of the real segment \(I=[0,1]\). It is built by induction:

• Starting with \(K_0=I\)
• If \(K_n\) is a finite disjoint union of segments \(K_n=\cup_k \left[a_k,b_k\right]\), \[K_{n+1}=\bigcup_k \left(\left[a_k,a_k+\frac{b_k-a_k}{3}\right] \cup \left[a_k+2\frac{b_k-a_k}{3},b_k\right]\right)\]

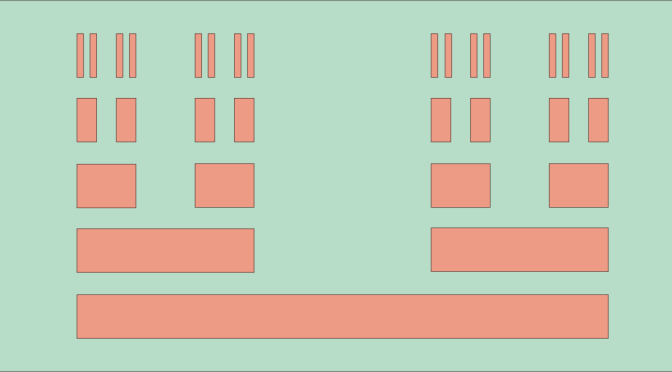
And finally \(K=\displaystyle \bigcap_{n \in \mathbb{N}} K_n\). The Cantor set is created by repeatedly deleting the open middle third of a set of line segments starting with the segment \(I\).

The Cantor set is a closed set as it is an intersection of closed sets.

The Cantor set has measure \(0\)

\(K_n\) is the disjoint union of \(2^n\) closed intervals of length \(3^{-n}\). As \(K \subset K_n\), we have \(\mu(K) \le \mu(K_n)=(\frac{2}{3})^n\) for all \(n \in \mathbb{N}\) where \(\mu(A)\) denotes the Lebesgue measure of a measurable subset \(A \subset \mathbb{R}\). Therefore \(\mu(K)=0\), i.e. \(K\) is a null set.

The Cantor set has the cardinality of the continuum

By induction, one can prove that for all \(n \in \mathbb{N}\):
\[K_n = \bigcup_{(\epsilon_1, \dots, \epsilon_n) \in \{0,2\}^n} \left[\sum_{k=1}^n \frac{\epsilon_k}{3^k},\frac{1}{3^n}+\sum_{k=1}^n \frac{\epsilon_k}{3^k}\right]\]
Let’s pick-up \(x \in [0,1]\) and consider its ternary representation \( \displaystyle x = \sum_{k=1}^\infty \alpha_k 3^{-k}\). For \((\epsilon_1, \dots, \epsilon_n) \in \{0,2\}^n\) we have the equivalence:
\[\sum_{k=1}^n \frac{\epsilon_k}{3^k} \le x < \frac{1}{3^n}+\sum_{k=1}^n \frac{\epsilon_k}{3^k} \Leftrightarrow \forall k \in \{1, \dots, n\}, \alpha_k = \epsilon_k\] In the case that \(x\) can be written \(x=\frac{1}{3^n}+\sum_{k=1}^n \frac{\epsilon_k}{3^k}\), we also have \(x = \sum_{k=1}^\infty \epsilon_k 3^{-k}\) with \(\epsilon_k = 2\) for all \(k \ge n+1\). Finally, \(x \in K\) if and only if there exist a sequence \((\epsilon_k) \in \{0,2\}^{\mathbb{N}^*}\) such that \(x = \sum_{k=1}^\infty \epsilon_k 3^{-k}\). In other words, \(x\) belongs to \(K\) if and only if its ternary representation (proper or improper) contains only the figures \(0\) and \(2\). To conclude on the cardinality of \(K\), we consider the function: \[\varphi : \left| \begin{array}{ll} [0,1) & \longrightarrow K\\ x=\sum_{k=1}^\infty \frac{\epsilon_k}{2^k} & \longmapsto \sum_{k=1}^\infty \frac{2 \epsilon_k}{3^k} \end{array} \right.\] \(\varphi\) is one-to-one. As \([0,1)\) has the cardinality of the continuum \(\mathfrak{c}\), \(K\) also has the cardinality of the continuum.