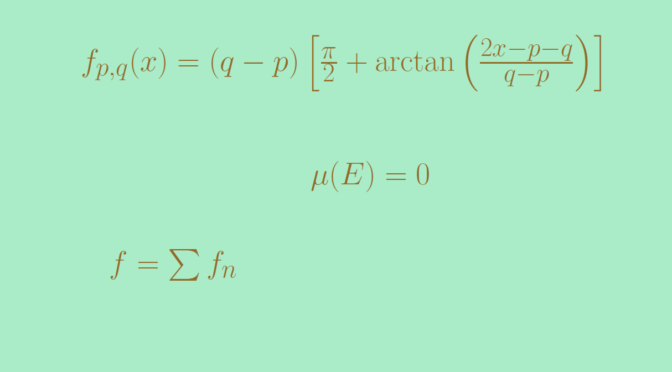We build in this article a strictly increasing continuous function \(f\) that is differentiable at no point of a null set \(E\). The null set \(E\) can be chosen arbitrarily. In particular it can have the cardinality of the continuum like the Cantor null set.

A set of strictly increasing continuous functions

For \(p \lt q\) two real numbers, consider the function \[
f_{p,q}(x)=(q-p) \left[\frac{\pi}{2} + \arctan{\left(\frac{2x-p-q}{q-p}\right)}\right]\] \(f_{p,q}\) is positive and its derivative is \[
f_{p,q}^\prime(x) = \frac{2}{1+\left(\frac{2x-p-q}{q-p}\right)^2}\] which is always strictly positive. Hence \(f_{p,q}\) is strictly increasing. We also have \[
\lim\limits_{x \to -\infty} f_{p,q}(x) = 0 \text{ and } \lim\limits_{x \to \infty} f_{p,q}(x) = \pi(q-p).\] One can notice that for \(x \in (p,q)\), \(f_{p,q}^\prime(x) \gt 1\). Therefore for \(x, y \in (p,q)\) distinct we have according to the mean value theorem \(\frac{f_{p,q}(y)-f_{p,q}(x)}{y-x} \ge 1\).

Covering \(E\) with an appropriate set of open intervals

As \(E\) is a null set, for each \(n \in \mathbb N\) one can find an open set \(O_n\) containing \(E\) and measuring less than \(2^{-n}\). \(O_n\) can be written as a countable union of disjoint open intervals as any open subset of the reals. Then \(I=\bigcup_{m \in \mathbb N} O_m\) is also a countable union of open intervals \(I_n\) with \(n \in \mathbb N\). The sum of the lengths of the \(I_n\) is less than \(1\).

\(I\) has following property.
Let \(x \in E\), \(U\) be a neighbourhood of \(x\) and let \(n \in \mathbb N\). Then there exist \(i_1 \lt \dots \lt i_n\) such that \(x \in I_{i_k} \subset U\) for each \(k \in \{1, \dots,n\}\).

Let’s prove it. As \(U\) is supposed to be open, one can find \(m \in \mathbb N\) large enough in order to have \((x-2^{-m-1},x+2^{-m-1}) \subset U\). Then \(x\) belongs to one of the open intervals \(I_{i_1}\) of \(O_{m+1}\). For that \(i_1\) we have \(I_{i_1} \subset U\) as the length of \(I_{i_1}\) is at most equal to \(2^{-(m+1)}\). The prove can then be completed by induction.

Defining the function \(f\)

Each open interval \(I_n\) of \(I\) can be written \(I_n=(p_n,q_n)\) with \(p_n \lt q_n\). For \(n \in \mathbb N\) we denote \(f_n=f_{p_n,q_n}\) and set \(f=\sum_{n=1}^\infty f_n\). For all \(x \in \mathbb R\) and \(n \in \mathbb N\) we have \[
0 \le f_n(x) \le \pi (q_n-p_n) = \pi \mu(I_n),\] where \(\mu\) denotes Lebesgue measure. By hypothesis, the series of positive numbers \(\sum \mu(I_n)\) converges (and its sum is less than one). Therefore the series of positive functions \(\sum f_n\) converges uniformly. Also \(f\) is continuous and strictly increasing as the \(f_n\) are all continuous and strictly increasing.

Let \(x \in E\). We show that \(f\) is not differentiable at \(x\). According to previous paragraph, for all \(m \in \mathbb N\) we can chose a sequence \(i_1 \lt \dots \lt i_m\) such that \(x \in I_{i_k}\) and \(I_{i_k} \subset (x -1/m,x+1/m)\) for each \(k \in \{1, \dots, m\}\). As \(I_{i_1} \cap \dots \cap I_{i_m}\) is an open subset containing \(x\), we can pick up \(y_m \in I_{i_1} \cap \dots \cap I_{i_m}\) distinct of \(x\). Then \[
\frac{f(y_m)-f(x)}{y_m-x} \ge \sum_{k=1}^m \frac{f_{i_k}(y_m)-f_{i_k}(x)}{y_m-x} \ge \sum_{k=1}^m 1 = m,\] according to the first paragraph. The sequence \((y_m)\) converges to \(x\) and \[
\lim\limits_{n \to \infty} \frac{f(y_m)-f(x)}{y_m-x} = \infty.\] This proves that \(f\) is not differentiable at \(x\).