In this article, I will describe a subset of the plane that is a connected space while not locally connected nor path connected.
Let’s consider the plane \(\mathbb{R}^2\) and the two subspaces:
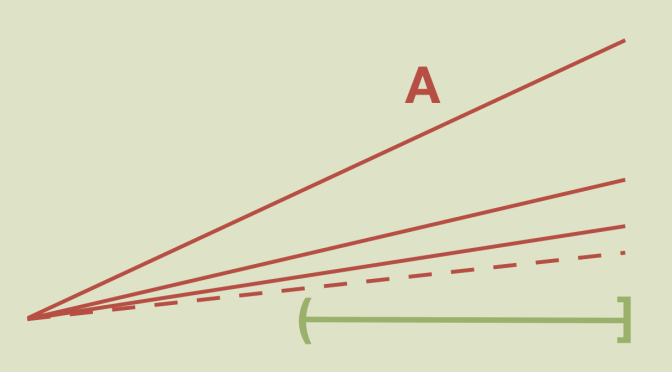
\[A = \bigcup_{n \ge 1} [(0,0),(1,\frac{1}{n})] \text{ and } B = A \cup (\frac{1}{2},1]\] Where a segment noted \(|a,b|\) stands for the plane segment \(|(a,0),(b,0)|\).
Let’s consider \(B\) and \(\overline{B}\) topological properties equipped with the subspace topology.
\(A\) and \(B\) are connected
It is well know that a path connected space is connected. Hence \(A\) is connected. If \(B\) wasn’t connected, \(B\) would be the disjoint union of two non empty open sets \(O_1\) and \(O_2\). As \(A\) is connected, \(A\) is the subset of \(O_1\) or \(O_2\). Let say \(A \subset O_1\). Also, \((\frac{1}{2},1]\) is connected. Hence \((\frac{1}{2},1] \subset O_2\) as \(O_2 \neq \emptyset\). Now any neighborhood of a point of \((\frac{1}{2},1]\) intersects \(A\) which is a contradiction.
We have \(\overline{B}=A \cup [0,1]\) and \(\overline{B}\) is connected
A point \((x,0) \in [0,1]\) is the limit of the sequence \(((x,\frac{x}{n}))_{n \ge 1}\). Therefore \(\overline{B}=A \cup [0,1]\). And \(\overline{B}\) is connected as the closure of a connected set.
\(\overline{B}\) is path connected while \(B\) is not
\(\overline{B}\) is path connected as any point in \(\overline{B}\) can be joined to the plane origin: consider the line segment joining the two points.
For the proof that \(B\) is not path connected, suppose that \(\gamma\) is a path joining the point \((\frac{3}{4},0)\) to the point \((1,1)\). We note \(\arg \gamma(t)\) the angle of \(\overrightarrow{\gamma(t)}\) with the X-axis. \(\arg \gamma(t)\) is a continuous function of \(t \in [0,1]\). Hence its range is connected (the image of a connected set under a continuous map is connected). This is in contradiction with the fact that \(\arg (1,1)\) is an isolated point of \(\arg(B)\).
Neither \(B\) nor \(\overline{B}\) is locally connected
The point \(P=((\frac{3}{4},0)\) belongs to \(B\). The intersection \(U\) of the open disk centered on \(P\) with radius \(\frac{1}{4}\) and \(B\) is an open of \(B\). As the origin doesn’t belong to \(U\), \(B\) and \(\overline{B}\) are not locally connected at \(P\).
Finally, \(B\) is connected, not locally connected and not path connected.

One thought on “A connected not locally connected space”