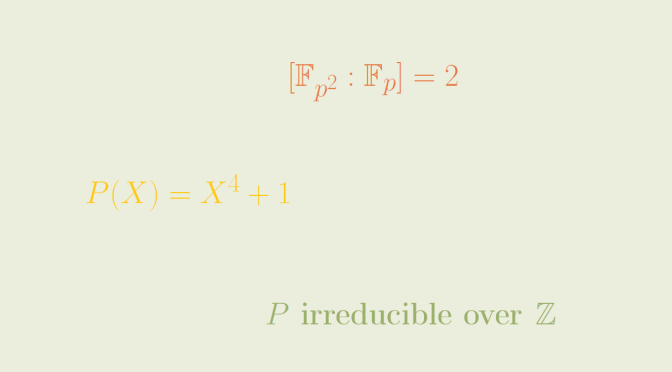A classical way to prove that an integral polynomial \(Q \in \mathbb{Z}[X]\) is irreducible is to prove that \(Q\) is irreducible over a finite prime field \(\mathbb{F}_p\) where \(p\) is a prime.

This raises the question whether an irreducible integral polynomial is irreducible over at least one finite prime field. The answer is negative and:
\[P(X)=X^4+1\] is a counterexample. Continue reading An irreducible integral polynomial reducible over all finite prime fields →