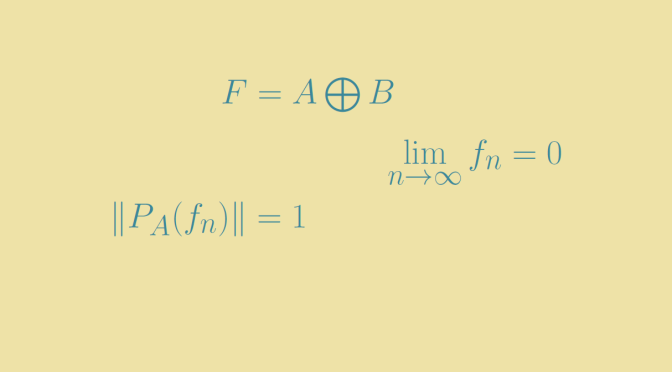We give here an example of a two complemented subspaces \(A\) and \(B\) that are not topologically complemented.
For this, we consider a vector space of infinite dimension equipped with an inner product. We also suppose that \(E\) is separable. Hence, \(E\) has an orthonormal basis \((e_n)_{n \in \mathbb N}\).
Let \(a_n=e_{2n}\) and \(b_n=e_{2n}+\frac{1}{2n+1} e_{2n+1}\). We denote \(A\) and \(B\) the closures of the linear subspaces generated by the vectors \((a_n)\) and \((b_n)\) respectively. We consider \(F=A+B\) and prove that \(A\) and \(B\) are complemented subspaces in \(F\), but not topologically complemented.
\(A\) and \(B\) are complemented subspaces in \(F\)
Let \(\langle \cdot , \cdot \rangle\) be the inner product. For \(i \neq j\) integers we have \(\langle a_i, a_j \rangle =0\) and \(\langle b_i, b_j \rangle =0\) as \((e_n)_{n \in \mathbb N}\) is an orthonormal basis. Therefore all \(x \in A\) can be written \(\displaystyle \sum_{n=0}^{+\infty} \langle x , e_{2n} \rangle e_{2n}\) and all \(x \in B\) can be written \(\displaystyle \sum_{n=0}^{+\infty} \langle x , b_n \rangle \frac{b_n}{\Vert b_n \Vert^2}\).
If \(x \in A \cap B\), we have for all \(n \in \mathbb N\) \(\langle x, e_{2n+1} \rangle =0\) as \(x \in A\). Hence \[x=\sum_{n=0}^{+\infty} \langle x , e_{2n} \rangle \frac{b_n}{\Vert b_n \Vert^2}\] Making the inner product of \(x\) with \(e_{2n+1}\) we get \[\langle x, e_{2n+1} \rangle = \langle x , e_{2n} \rangle \frac{\Vert e_{2n+1} \Vert^2}{(2n+1)\Vert b_n \Vert^2} = 0\] Consequently, we have \(\langle x, e_{2n} \rangle\) for all \(n \in \mathbb N\) and finally \(x = 0\) which proves that \(A\) and \(B\) are complemented subspaces in \(F\).
\(A\) and \(B\) are not topologically complemented
Let \((x_n)\) be the sequence \(x_n = b_n-a_n\). We have \(x_n=\frac{e_{2n+1}}{n+1}\) and \(\lim\limits_{n \to \infty} x_n = 0\). If \(A\) and \(B\) were topologically complemented, the projection of \(F\) on the subspace \(A\) would be continuous. But the projection of \(x_n\) is \(a_n\) as \(A\) and \(B\) are complemented subspaces. However \(\Vert a_n \Vert = 1\) for all \(n \in \mathbb N\) as \((e_n)\) is an orthonormal basis. A contradiction proving that \(A\) and \(B\) are not topologically complemented.